题目内容
如图1,四边形OABC中,OA=a,OC=3,BC=2,∠AOC=∠BCO=90°,经过点O的直线l将四边形分成两部分,直线l与OC所成的角设为θ,将四边形OABC的直角∠OCB沿直线l折叠![]() ,点C落在
,点C落在![]() 点D处(如图1).
点D处(如图1).
(1)若折叠![]() 后点D恰为AB的中点(如图2),则θ= ;
后点D恰为AB的中点(如图2),则θ= ;
(2)若θ=45°,四边形OABC的直角∠OCB沿直线l折叠![]() 后,点B落在点四边形OABC的边AB上的E处(如图3),求a的值;
后,点B落在点四边形OABC的边AB上的E处(如图3),求a的值;
 |
(1)∴θ=30°;(3分)
(2)若点E四边形0ABC的边AB上,
 ∴AB⊥直线l (4分)
∴AB⊥直线l (4分)
由折叠可知,OD=OC=3,DE=BC=2.(6分)
∵θ=45°,AB⊥直线l,
∴△ADE为等腰直角三角形,(7分)
∴AD=DE=2,(8分)
∴OA=OD+AD=3+2=5,
∴a=5;(9分)

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 21、已知:如图,在Rt△OAB中,∠OAB=90°,OA=AB=6cm,将△OAB绕点O沿逆时针方向旋转90°得到Rt△OA1B1
21、已知:如图,在Rt△OAB中,∠OAB=90°,OA=AB=6cm,将△OAB绕点O沿逆时针方向旋转90°得到Rt△OA1B1 (2011•台州模拟)如图等腰三角形纸片OAB,现要求在纸片上截一个正方形,使它的面积尽可能大.
(2011•台州模拟)如图等腰三角形纸片OAB,现要求在纸片上截一个正方形,使它的面积尽可能大.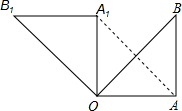 到△OA1B1.
到△OA1B1. 如图所示,△OAB绕点O旋转l80°得到△OCD,连接AD,BC,得到四边形ABCD.
如图所示,△OAB绕点O旋转l80°得到△OCD,连接AD,BC,得到四边形ABCD. (2009•株洲)如图,在Rt△OAB中,∠OAB=90°,OA=AB=6,将△OAB绕点O沿逆时针方向旋转90°得到△OA1B1.
(2009•株洲)如图,在Rt△OAB中,∠OAB=90°,OA=AB=6,将△OAB绕点O沿逆时针方向旋转90°得到△OA1B1.