Question

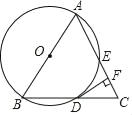
【题目】如图，等腰直角三角形 AEF 的顶点 E 在等腰直角三角形 ABC 的边 BC上．AB 的延长线交 EF 于 D 点，其中∠AEF＝∠ABC＝90°．

(1)求证：

(2)若 E 为 BC 的中点，求的值．

Answer 1

【答案】（1）见解析；（2）

【解析】

（1）由△AEF、△ABC是等腰直角三角形，易证得△FAD∽△CAE，然后由相似三角形的对应边成比例，可得 ，又由等腰直角三角形的性质，可得AF= AE，即可证得；

（2）首先设BE=a，由射影定理，可求得DB的长，继而可求得DA的长，即可求得答案．

(1)证明：∵△AEF、△ABC是等腰直角三角形，

∴∠EAF=∠BAC=45°,∠F=∠C=45°，

∴∠FAD=∠CAE，

∴△FAD∽△CAE，

∴，

∵∠AEF=90°，AE=EF，

∴AF=AE，

∴；

(2)设BE=a，

∵E为BC的中点，

∴EC=BE=a，AB=BC=2a，

∵∠AEF=∠ABC=90°，

∴BE =ABDB，

∴DB= ，

∵DA=DB+AB，

∴DA= ，

∴= .