题目内容
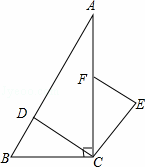
如图，在Rt△ABC中，∠ACB=90°，点D、F分别在AB、AC上，CF=CB，连接CD，将线段CD绕点C按顺时针方向旋转90°后得CE，连接EF．
（1）求证：△BCD≌△FCE；
（2）若EF∥CD，求∠BDC的度数．
（1）证明：∵将线段CD绕点C按顺时针方向旋转90°后得CE，
∴CD=CE，∠DCE=90°，
∵∠ACB=90°，
∴∠BCD=90°﹣∠ACD=∠FCE，
在△BCD和△FCE中，
，
∴△BCD≌△FCE（SAS）．
（2）解：由（1）可知△BCD≌△FCE，
∴∠BDC=∠E，
∵EF∥CD，
∴∠E=180°﹣∠DCE=90°，
∴∠BDC=90°．
练习册系列答案
相关题目
有一个根为
，且关于x的方程ax 2＋bx＋9＝ 
x
有两个相等的实数根，求
、
的值．为了解九年级学生的视力情况，某校随机抽取50名学生进行视力检查，结果如下：
| 视力 | 4.6以下 | 4.6 | 4.7 | 4.8 | 4.9 | 5.0 | 5.0以上 |
| 人数（人） | 6 | 15 | 5 | 10 | 3 | 4 | 7 |
这组数据的中位数是（ ）．
A．4.6 B．4.7 C．4.8 D．4.9
