题目内容
如图所示,AB是⊙O的直径,弦CD⊥AB于P,已知CD=8cm,∠B=30°,求⊙O的半径.
【答案】分析:连接OC.根据直角三角形中30°的角所对直角边是斜边的一半和勾股定理解答.
解答: 解:方法一:连接OC,
解:方法一:连接OC,
∵AB是⊙O的直径,AB⊥CD于P,CD=8,
∴CP= CD=4,
CD=4,
又∠B=30°,∴∠AOC=2∠B=60°,∠OCP=30°,
设⊙O的半径为R,则OC=R,OP= R,
R,
在Rt△COP中,( R)2+42=R2,解得R=
R)2+42=R2,解得R=
 ,
,
故⊙O的半径为
 cm,
cm,
方法二:∵AB是⊙O的直径,AB⊥CD于P,CD=8,
∴∠ACB=90°,∠A=90°-∠B=60°,CP= CD=4,∠ACP=30°,则AC=2AP,
CD=4,∠ACP=30°,则AC=2AP,
在Rt△ACP中,AP2+CP2=AC2,即AP2+42=(2AP)2,解得AP=
 (舍负),
(舍负),
又OA=OC,∴△AOC是等边三角形,
∴AC=2AP=
 ,故⊙O的半径为
,故⊙O的半径为
 cm.
cm.
点评:此题结合了勾股定理、直角三角形的性质和垂径定理,至少可有两种方法.
解答:
 解:方法一:连接OC,
解:方法一:连接OC,∵AB是⊙O的直径,AB⊥CD于P,CD=8,
∴CP=
 CD=4,
CD=4,又∠B=30°,∴∠AOC=2∠B=60°,∠OCP=30°,
设⊙O的半径为R,则OC=R,OP=
 R,
R,在Rt△COP中,(
 R)2+42=R2,解得R=
R)2+42=R2,解得R=
 ,
,故⊙O的半径为

 cm,
cm,方法二:∵AB是⊙O的直径,AB⊥CD于P,CD=8,
∴∠ACB=90°,∠A=90°-∠B=60°,CP=
 CD=4,∠ACP=30°,则AC=2AP,
CD=4,∠ACP=30°,则AC=2AP,在Rt△ACP中,AP2+CP2=AC2,即AP2+42=(2AP)2,解得AP=

 (舍负),
(舍负),又OA=OC,∴△AOC是等边三角形,
∴AC=2AP=

 ,故⊙O的半径为
,故⊙O的半径为
 cm.
cm.点评:此题结合了勾股定理、直角三角形的性质和垂径定理,至少可有两种方法.

练习册系列答案
相关题目
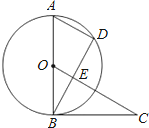 如图所示,AB是⊙O的直径,AD是弦,∠DBC=∠A.
如图所示,AB是⊙O的直径,AD是弦,∠DBC=∠A.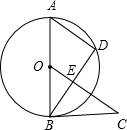 如图所示,AB是⊙O的直径,AD是弦,∠DBC=∠A,OC⊥BD于点E.
如图所示,AB是⊙O的直径,AD是弦,∠DBC=∠A,OC⊥BD于点E.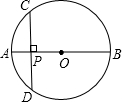 如图所示,AB是⊙O的直径,弦CD⊥AB于点P,CD=10cm,AP:PB=1:5,则⊙O的半径为
如图所示,AB是⊙O的直径,弦CD⊥AB于点P,CD=10cm,AP:PB=1:5,则⊙O的半径为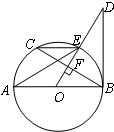 如图所示,AB是⊙O直径,OD⊥弦BC于点F,且交⊙O于点E,且∠AEC=∠ODB.
如图所示,AB是⊙O直径,OD⊥弦BC于点F,且交⊙O于点E,且∠AEC=∠ODB. 如图所示,AB是⊙O直径,∠D=35°,则∠BOC等于( )
如图所示,AB是⊙O直径,∠D=35°,则∠BOC等于( )