题目内容
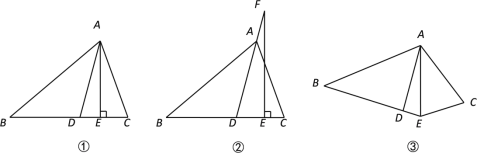
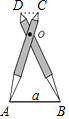
【题目】如图是小华利用含30°角的三角板测量楼房高度的示意图,已知桌子高AB为1米,地面上B和D之间的距离为100米,则楼高CD约为( ) 
A.51米
B.59米
C.88米
D.174米
【答案】B
【解析】解:过点A作AE⊥CD,垂足为E, 
∵AB⊥BD,DE⊥BD,AE∥BD,
∴四边形ABDE是矩形,
∵BD=100m,AB=1m,
∴AE=BD=100m,DE=AB=1m,
在Rt△ACE中,
∵∠CAE=30°,AE=100m,
∴CE=ADtan30°=100× ![]() =
= ![]() m,
m,
∴CD=CE+DE= ![]() +1≈59(m).
+1≈59(m).
答:楼高CD约为59m,
故选B.
【考点精析】掌握相似三角形的应用是解答本题的根本,需要知道测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
【题目】某校举行了“文明在我身边”摄影比赛.已知每幅参赛作品成绩记为x分(60≤x<100).校方从600幅参赛作品中随机抽取了部分参赛作品,统计了它们的成绩,并绘制了如下不完整的统计图表.
分数段 | 频数 | 频率 |
60≤x<70 | 18 | 0.36 |
70≤x<80 | 17 | c |
80≤x<90 | a | 0.24 |
90≤x<100 | b | 0.06 |
合计 | 1 |

根据以上信息解答下列问题:
(1)统计表中c的值为________;样本成绩的中位数落在分数段________中;
(2)补全频数直方图;
(3)若80分以上(含80分)的作品将被组织展评,试估计全校被展评的作品数量是多少.