题目内容
△ABC中,点O为∠ABC和∠ACB角平分线交点,则∠BOC与∠A的关系是
- A.∠BOC=2∠A
- B.∠BOC=180°-
 ∠A
∠A - C.∠BOC=90°+
 ∠A
∠A - D.∠BOC=90°+∠A
C
分析:根据三角形的内角和定理和角平分线的定义求∠BOC与∠A的关系即可.
解答:∠BOC=180°-(∠OBC+∠OCB)=180°- (∠ABC+∠ACB)=180°-
(∠ABC+∠ACB)=180°- (180°-∠A)=90°+
(180°-∠A)=90°+ ∠A.
∠A.
故选C.
点评:此题主要是根据三角形的内角和定理结合角平分线的定义进行推导.
分析:根据三角形的内角和定理和角平分线的定义求∠BOC与∠A的关系即可.
解答:∠BOC=180°-(∠OBC+∠OCB)=180°-
 (∠ABC+∠ACB)=180°-
(∠ABC+∠ACB)=180°- (180°-∠A)=90°+
(180°-∠A)=90°+ ∠A.
∠A.故选C.
点评:此题主要是根据三角形的内角和定理结合角平分线的定义进行推导.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


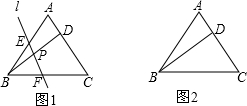
 如图,在△ABC中,点D为BC上一点,点P在AD上,过点P作PM∥AC交AB于点M,作PN∥AB交AC于点N.
如图,在△ABC中,点D为BC上一点,点P在AD上,过点P作PM∥AC交AB于点M,作PN∥AB交AC于点N.
 如图,在△ABC中,点D为BC的中点,点E为AB上一点,DF⊥DE交AC于F,延长ED至G,使ED=GD.
如图,在△ABC中,点D为BC的中点,点E为AB上一点,DF⊥DE交AC于F,延长ED至G,使ED=GD.