题目内容
17.设x-y=1+a,y-z=1-a,求x2-xy-yz-xz+y2+z2的值.分析 由x-y=1+a,y-z=1-a易得x-z=2,然后把x2+y2+z2-xy-yz-xz进行变形得到$\frac{1}{2}$(2x2+2y2+2z2-2xy-2yz-2xz),根据完全平方公式分组分解为$\frac{1}{2}$[(x-y)2+(y-z)2+(x-z)2],再代值计算即可.
解答 解:∵x-y=1+a,y-z=1-a,
∴x-z=2,
∴x2+y2+z2-xy-yz-xz
=$\frac{1}{2}$(2x2+2y2+2z2-2xy-2yz-2xz
=$\frac{1}{2}$[(x-y)2+(y-z)2+(x-z)2]
=$\frac{1}{2}$[(1+a)2+(1-a)2+22]
=a2+3.
点评 此题考查因式分解的实际运用,掌握完全平方公式:(a±b)2=a2±2ab+b2是解决问题的关键.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
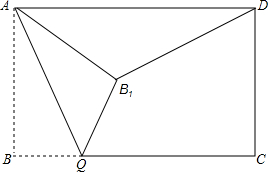 如图,长方形ABCD中AB=2,BC=4,点Q是线段BC上一点,连接AQ,作点B关于直线AQ的对称点B,连接AB1,QB1.
如图,长方形ABCD中AB=2,BC=4,点Q是线段BC上一点,连接AQ,作点B关于直线AQ的对称点B,连接AB1,QB1. 如图,已知AB∥A′B′,BC∥B′C′,那么∠B与∠B′有何关系?为什么?
如图,已知AB∥A′B′,BC∥B′C′,那么∠B与∠B′有何关系?为什么? 如图,AE=CF,AD∥BC,AD=CB.求证:△ADF≌△CBE.
如图,AE=CF,AD∥BC,AD=CB.求证:△ADF≌△CBE. 如图,矩形ABCD中,AB=6,BC=$2\sqrt{3}$,点O是AB的中点,点P在AB的延长线上,且BP=3.一动点E从O点出发,以每秒1个单位长度的速度沿OA匀速运动,到达A点后,立即以原速度沿AO返回;另一动点F从P点出发,以每秒1个单位长度的速度沿射线PA匀速运动,点E、F同时出发,当两点相遇时停止运动,在点E、F的运动过程中,以EF为边作等边△EFG,使△EFG和矩形ABCD在射线PA的同侧.设运动的时间为t秒(t≥0).
如图,矩形ABCD中,AB=6,BC=$2\sqrt{3}$,点O是AB的中点,点P在AB的延长线上,且BP=3.一动点E从O点出发,以每秒1个单位长度的速度沿OA匀速运动,到达A点后,立即以原速度沿AO返回;另一动点F从P点出发,以每秒1个单位长度的速度沿射线PA匀速运动,点E、F同时出发,当两点相遇时停止运动,在点E、F的运动过程中,以EF为边作等边△EFG,使△EFG和矩形ABCD在射线PA的同侧.设运动的时间为t秒(t≥0).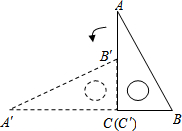 如图,直角三角板ABC,AC=10,BC=5,绕点C沿逆时针方向旋转90°至△A′B′C′,再沿CB向右平移,使点B′刚好落在斜边AB上,此三角板向右平移时,△A′B′C′扫过的面积是12.5cm2.
如图,直角三角板ABC,AC=10,BC=5,绕点C沿逆时针方向旋转90°至△A′B′C′,再沿CB向右平移,使点B′刚好落在斜边AB上,此三角板向右平移时,△A′B′C′扫过的面积是12.5cm2.