题目内容
14、函数y1=-x2+2x+4,y2=x+2,则使y1≥y2的x的取值范围是
-1≤x≤2
.分析:先把二次函数配成顶点式,然后在同一直角坐标系中画出y1=-x2+2x+4,y2=x+2的图象,利用解方程求出它们交点的横坐标,再观察函数图象可确定使y1≥y2的x的取值范围.
解答:解:y1=-x2+2x+4=-(x-1)2+5,
在同一直角坐标系中画出y1=-x2+2x+4,y2=x+2的图象,如图,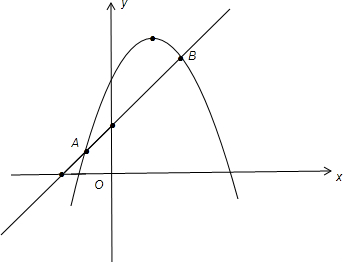
解方程-x2+2x+4=x+2得x=-1或2,
所以A点和B点的横坐标分别为-1,2.
当y1>y2,即抛物线在一次函数图象上方所对应的自变量的取值范围为-1<x<2,
所以使y1≥y2的x的取值范围是-1≤x≤2.
故答案为-1≤x≤2.
在同一直角坐标系中画出y1=-x2+2x+4,y2=x+2的图象,如图,

解方程-x2+2x+4=x+2得x=-1或2,
所以A点和B点的横坐标分别为-1,2.
当y1>y2,即抛物线在一次函数图象上方所对应的自变量的取值范围为-1<x<2,
所以使y1≥y2的x的取值范围是-1≤x≤2.
故答案为-1≤x≤2.
点评:本题考查了利用二次函数和一次函数图象解不等式的方法:先画出反映不等式的两函数图象,再利用方程组求出两函数图象的交点的坐标,然后观察图象得到满足不等式的自变量的取值范围.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
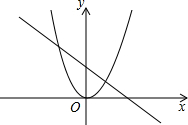 已知函数y1=x2与函数y2=-
已知函数y1=x2与函数y2=-| 1 |
| 2 |
A、-
| ||
B、x>2或x<-
| ||
C、-2<x<
| ||
D、x<-2或x>
|
 函数y1=x2+1与
函数y1=x2+1与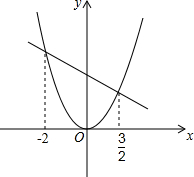 (2011•赣州模拟)已知函数y1=x2与y2=-
(2011•赣州模拟)已知函数y1=x2与y2=- 二次函数
二次函数