题目内容
 如图,CD=BE,DG⊥BC,EF⊥BC,垂足分别为G,F,且DG=EF.
如图,CD=BE,DG⊥BC,EF⊥BC,垂足分别为G,F,且DG=EF.(1)△DGC与△EFB全等吗?请说明理由;
(2)OB=OC吗?请说明理由;
(3)若∠B=30°,判断△ADO的形状(直接写出答案)
分析:(1)由于DG⊥BC,EF⊥BC,可知∠DGC=∠EFB=90°,而CD=BE,DG=EF,利用HL易证Rt△EFB≌Rt△DGC;
(2)由(1)知Rt△EFB≌Rt△DGC,根据全等三角形的性质可知∠B=∠C,从而可知OB=OC;
(3)由∠B=30°易知∠C=30°,从而可知∠D=60°,在Rt△ABG中,∠B=30°,易求∠BAG=60°,即∠DAO=60°,从而易证△ADO是等边三角形.
(2)由(1)知Rt△EFB≌Rt△DGC,根据全等三角形的性质可知∠B=∠C,从而可知OB=OC;
(3)由∠B=30°易知∠C=30°,从而可知∠D=60°,在Rt△ABG中,∠B=30°,易求∠BAG=60°,即∠DAO=60°,从而易证△ADO是等边三角形.
解答:解:(1)△DGC≌△EFB,
∵DG⊥BC,EF⊥BC,
∴∠DGC=∠EFB=90°,
在Rt△EFB和Rt△DGC中,
CD=BE,DG=EF,
∴Rt△EFB≌Rt△DGC;
(2)OB=OC,
由(1)知Rt△EFB≌Rt△DGC,
∴∠B=∠C,
∴OB=OC;
(3)△ADO是等边三角形.

∵DG⊥BC,EF⊥BC,
∴∠DGC=∠EFB=90°,
在Rt△EFB和Rt△DGC中,
CD=BE,DG=EF,
∴Rt△EFB≌Rt△DGC;
(2)OB=OC,
由(1)知Rt△EFB≌Rt△DGC,
∴∠B=∠C,
∴OB=OC;
(3)△ADO是等边三角形.
点评:本题考查了全等三角形的判定和性质、直角三角形的判定和性质、等边三角形的判定、等腰三角形的性质.解题的关键是证明Rt△EFB≌Rt△DGC.

练习册系列答案
相关题目
 24、如图,CD∥BE,∠1=20°,∠2=60°,则∠3=
24、如图,CD∥BE,∠1=20°,∠2=60°,则∠3= 与
与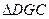 与
与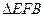 全等吗?请说明理由;
全等吗?请说明理由;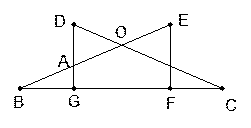

 与
与 全等吗?请说明理由;(4分)
全等吗?请说明理由;(4分) 的形状是 (2分)
的形状是 (2分)