题目内容
【题目】设A＝
÷（a﹣
）．
（1）化简A；
（2）当a＝3时，记此时A的值为f（3）；当a＝4时，记此时A的值为f（4）；…解关于x的不等式：
≤f（3）+f（4）+…+f（11），并将解集在数轴上表示出来．
【答案】（1）
；（2）x≤4．
【解析】
（1）根据分式的混合运法则可以解答本题；
（2）根据（1）中的结果可以解答题目中的不等式，并在数轴上表示出不等式的解集．
（1）A=
÷（a﹣
）
=
=
=
=
=；
（2）∵a=3时，f（3）=
，a=4时，f（4）=
，a=5时，f（5）=
，…
∴
﹣
≤f（3）+f（4）+…+f（11），即﹣≤
+
+…+
∴﹣≤
+…+
﹣≤
﹣≤
，
解得：x≤4，∴原不等式的解集是x≤4，在数轴上表示如下所示：
．
【题目】列方程解应用题：五莲县新玛特购物中心第一次用5000元购进甲、乙两种商品，其中乙商品的件数比甲商品件数的
倍多15件，甲、乙两种商品的进价和售价如下表（注：获利=售价﹣进价）
甲 | 乙 | |
进价（元/件） | 20 | 30 |
售价（元/件） | 29 | 40 |
（1）新玛特购物中心将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润？
（2）该购物中心第二次以第一次的进价又购进甲、乙两种商品，其中甲种商品的件数不变，乙种商品的件数是第一次的3倍；甲商品按原价销售，乙商品打折销售，第二次两种商品都销售完以后获得总利润比第一次获得的总利润多160元，求第二次乙种商品是按原价打几折销售？
【题目】网上购物已经成为人们常用的一种购物方式，售后评价特别引人关注，为了解市民对售后评价的关注情况，随机采访部分市民，对采访情况制作了如下统计图表：
关注情况 | 频数 | 频率 |
A．高度关注 | 50 | b |
B．一般关注 | 120 | 0.6 |
C．不关注 | a | 0.1 |
D．不知道 | 10 | 0.05 |
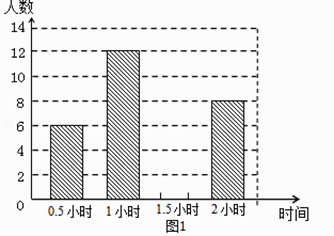
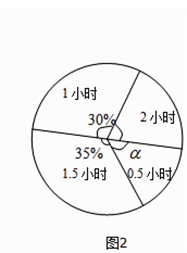
（1）根据上述统计图可得此次采访的人数为人，a= ， b=；
（2）根据以上信息补全条形统计图；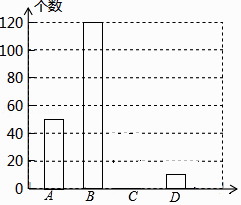 
（3）根据上述采访结果，请估计在6400名市民中，高度关注售后评价的市民约有多少人？
