题目内容
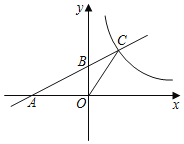
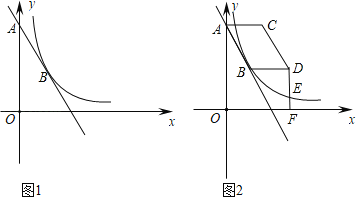
【题目】如图1,点![]() 、点
、点![]() 在直线
在直线![]() 上,反比例函数
上,反比例函数![]() (
(![]() )的图象经过点
)的图象经过点![]() .
.
(1)求![]() 和
和![]() 的值;
的值;
(2)将线段![]() 向右平移
向右平移![]() 个单位长度(
个单位长度(![]() ),得到对应线段
),得到对应线段![]() ,连接
,连接![]() 、
、![]() .
.
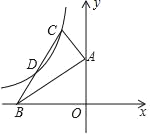
①如图2,当![]() 时,过
时,过![]() 作
作![]() 轴于点
轴于点![]() ,交反比例函数图象于点
,交反比例函数图象于点![]() ,求
,求![]() 的值;
的值;
②在线段![]() 运动过程中,连接
运动过程中,连接![]() ,若
,若![]() 是以
是以![]() 为腰的等腰三形,求所有满足条件的
为腰的等腰三形,求所有满足条件的![]() 的值.
的值.
【答案】(1)![]() ,
,![]() ;(2)①
;(2)①![]() ;②
;②![]() 是以
是以![]() 为腰的等腰三形,满足条件的
为腰的等腰三形,满足条件的![]() 的值为4或5.
的值为4或5.
【解析】
(1)先将点![]() 坐标代入直线
坐标代入直线![]() 的解析式中,求出
的解析式中,求出![]() ,进而求出点
,进而求出点![]() 坐标,再将点
坐标,再将点![]() 坐标代入反比例函数解析式中即可得出结论;
坐标代入反比例函数解析式中即可得出结论;
(2)①先确定出点![]() ,进而求出点
,进而求出点![]() 坐标,进而求出
坐标,进而求出![]() ,
,![]() ,即可得出结论;
,即可得出结论;
②先表示出点![]() ,
,![]() 坐标,再分两种情况:Ⅰ、当
坐标,再分两种情况:Ⅰ、当![]() 时,判断出点
时,判断出点![]() 在
在![]() 的垂直平分线上,即可得出结论;
的垂直平分线上,即可得出结论;
Ⅱ、当![]() 时,先表示出
时,先表示出![]() ,用
,用![]() 建立方程求解即可得出结论.
建立方程求解即可得出结论.
(1)∵点![]() 在直线
在直线![]() 上,
上,
∴![]() ,
,
∴![]() ,
,
∴直线![]() 的解析式为
的解析式为![]() ,
,
将点![]() 代入直线
代入直线![]() 的解析式
的解析式![]() 中,得
中,得![]() ,
,
∴![]() ,
,
∴![]() ,
,
将![]() 在反比例函数解析式
在反比例函数解析式![]() (
(![]() )中,得
)中,得![]() ;
;
(2)①由(1)知,![]() ,
,![]() ,∴反比例函数解析式为
,∴反比例函数解析式为![]() ,
,
当![]() 时,
时,
∴将线段![]() 向右平移3个单位长度,得到对应线段
向右平移3个单位长度,得到对应线段![]() ,
,
∴![]() ,
,
即:![]() ,
,
∵![]() 轴于点
轴于点![]() ,交反比例函数
,交反比例函数![]() 的图象于点
的图象于点![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴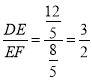 ;
;
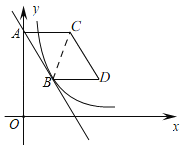
②如图,∵将线段![]() 向右平移
向右平移![]() 个单位长度(
个单位长度(![]() ),得到对应线段
),得到对应线段![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() 是以
是以![]() 腰的等腰三形,
腰的等腰三形,
∴Ⅰ、当![]() 时,
时,
∴![]() ,
,
∴点![]() 在线段
在线段![]() 的垂直平分线上,
的垂直平分线上,
∴![]() ,
,
Ⅱ、当![]() 时,
时,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
即:![]() 是以
是以![]() 为腰的等腰三形,满足条件的
为腰的等腰三形,满足条件的![]() 的值为4或5.
的值为4或5.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案
相关题目