Question

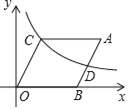
【题目】如图，ABOC放置在直角坐标系中，点A(10，4)，点B(6，0)，反比例函数y＝(x＞0)的图象经过点C．

(1)求该反比例函数的表达式．

(2)记AB的中点为D，请判断点D是否在该反比例函数的图象上，并说明理由．

(3)若P(a，b)是反比例函数y＝的图象(x＞0)的一点，且S△POC＜S△DOC，则a的取值范围为_____．

Answer 1

【答案】(1)y＝；(2)D点在反比例函数图象上；(3)2＜a＜4或4＜a＜8

【解析】

根据题意可得，可得C点坐标，则可求反比例函数解析式
根据题意可得D点坐标，代入解析式可得结论．
由图象可发现，，的面积和等于ABCD的面积一半，即，分点P在OC上方和下方讨论，设，用a表示的面积可得不等式，可求a的范围．

解：(1)∵ABOC是平行四边形

∴AC＝BO＝6

∴C(4，4)

∵反比例函数y＝(x＞0)的图象经过点C．

∴4＝

∴k＝16

∴反比例函数解析式y＝

(2)∵点A(10，4)，点B(6，0)，

∴AB的中点D(8，2)

当x＝8时，y＝＝2

∴D点在反比例函数图象上．

(3)根据题意当点P在OC的上方，作PF⊥y轴，CE⊥y轴

设P(a，)

S△COD＝SABOC﹣S△ACD﹣S△OBD

∴S△COD＝SABOC＝12

∵S△POC＜S△COD

∴，

∴a＞2或a＜﹣8(舍去)

当点P在OC的下方，则易得4＜a＜8

综上所述：2＜a＜4或4＜a＜8