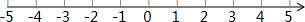Question

10．如图，抛物线的顶点为A（2，1），且经过原点O，与x轴的另一个交点为B．
（1）求抛物线的解析式；
（2）求当y＞0时，x的取值范围；
（3）在抛物线上求点M，使△MOB的面积是△AOB面积的3倍．

Answer 1

分析 （1）已知了抛物线的顶点坐标，可将其解析式设为顶点坐标式，然后将原点坐标代入上式，即可求得待定系数的值，从而确定该抛物线的解析式．
（2）求得抛物线与x轴的交点，即可求得当y＞0时，x的取值范围；
（3）由于△MOB和△AOB同底不等高，因此它们的面积比等于高的比，即M点的纵坐标的绝对值是A点纵坐标绝对值的3倍，由于A是抛物线顶点，因此点M必在x轴下方，将其纵坐标代入抛物线的解析式中，即可确定M点的坐标．

解答 解：（1）由题意，可设抛物线的解析式为y=a（x-2）²+1，
∵抛物线过原点，
∴a（0-2）²+1=0，a=-$\frac{1}{4}$；（2分）
∴抛物线的解析式为y=-$\frac{1}{4}$（x-2）²+1=-$\frac{1}{4}$x²+x．

（2）令y=0，则-$\frac{1}{4}$x²+x=0，解得x₁=0，x₂=4，
∴B（4，0），
∴当y＞0时，0＜x＜4．

（3）△AOB和所求△MOB同底不等高，且S_△MOB=3S_△AOB，
∴△MOB的高是△AOB高的3倍，
即M点的纵坐标是-3，
∴-3=-$\frac{1}{4}$x²+x，
即x²-4x-12=0，
解得x₁=6，x₂=-2，
∴满足条件的点有两个：M₁（6，-3），M₂（-2，-3）．

点评 此题主要考查了二次函数解析式的确定、图形面积的求法、函数图象上点的坐标意义等知识，难度不大，能够将图形的面积比转化为M点的纵坐标是解决（3）题的关键．