题目内容
海上有一座灯塔P,一客轮以60海里/时的速度由西向东航行,行至A处时测得灯塔P在北偏东60°方向,继续航行40分钟后,到B处又测得灯塔P在在北偏东60°方向,

(1)客轮在B距灯塔P多少海里?
(2)若在灯塔周围30海里有暗礁,客轮继续航行是否有触礁危险?
(1)客轮在B距灯塔40海里.(2)客轮继续向东航行无触礁危险.
【解析】
试题分析:(1)作PH⊥AC于点H,根据等腰三角形的判定与性质,可得AB=BP,再根据路程=速度×时间即可求出客轮在B处距离灯塔P的长;
(2)本题实际上是问,P到AB的距离即CD是否大于30,如果大于则无触礁危险,反之则有,根据三角函数可求PH的值,进行比较即可求解.
试题解析:(1)作PH⊥AC于点H

由题意可知∠PAB=30°,∠PBC=60°,
∴∠PAB=∠APB=30°,
∴AB=BP=60× =40海里.
=40海里.
∴客轮在B距灯塔40海里.
(2)由题意可知∠BPH=30°,
∵cos∠BPH=
∴
∴PH=20 ≈34.64
≈34.64
∵34.64>30
∴客轮继续向东航行无触礁危险.
考点:解直角三角形的应用-方向角问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

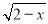 有意义,则x的取值范围是( )
有意义,则x的取值范围是( )

 (
( )与抛物线C2:
)与抛物线C2: ,
, 轴交于点A,其对称轴与
轴交于点A,其对称轴与 轴交于点B.求点A,B的坐标;
轴交于点B.求点A,B的坐标; 这一段位于C2下方,并且抛物线C1在
这一段位于C2下方,并且抛物线C1在 这一段位于C2上方,求抛物线C1的解析式.
这一段位于C2上方,求抛物线C1的解析式.