题目内容
△ABC中，AD是中线，AB=6，AD=13，则AC的取值范围为________．
20＜AC＜32
分析：先作辅助线，延长AD至点E，使DE=AD，连接EC，先证明△ABD≌△ECD，在△AEC中，由三角形的三边关系定理得出答案．
解答：延长AD至点E，使DE=AD，连接EC，
在△ABD和△ECD中，
，
∴△ABD≌△ECD（SAS），
∴CE=AB，
∵AB=6，AD=13，
∴AE=26，
∴26-6＜AC＜26+6，
∴20＜AC＜32．
故答案为：20＜AC＜32．
点评：此题主要考查了全等三角形的判定与性质以及学生对三角形三边关系及中线的性质等的理解及运用能力，得出△ABD≌△ECD是解题关键．
分析：先作辅助线，延长AD至点E，使DE=AD，连接EC，先证明△ABD≌△ECD，在△AEC中，由三角形的三边关系定理得出答案．
解答：延长AD至点E，使DE=AD，连接EC，
在△ABD和△ECD中，
，∴△ABD≌△ECD（SAS），
∴CE=AB，
∵AB=6，AD=13，
∴AE=26，
∴26-6＜AC＜26+6，
∴20＜AC＜32．
故答案为：20＜AC＜32．
点评：此题主要考查了全等三角形的判定与性质以及学生对三角形三边关系及中线的性质等的理解及运用能力，得出△ABD≌△ECD是解题关键．
练习册系列答案
口算题卡加应用题集训系列答案
综合自测系列答案
相关题目
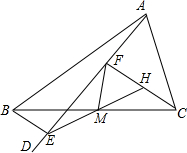如图，△ABC中，AD是∠BAC内的一条射线，BE⊥AD，且△CHM可由△BEM旋转而得，延长CH交AD于F，则下列结论错误的是（ ）| A、BM=CM | ||
B、FM=
| ||
| C、CF⊥AD | ||
| D、FM⊥BC |
在△ABC中，AD是BC上的高，且AD=
BC，E，F分别是AB，AC的中点，以EF为直径的圆与BC的位置关系是（ ）
| 1 |
| 2 |
| A、相离 | B、相切 |
| C、相交 | D、相切或相交 |
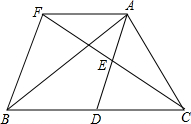如图，在△ABC中，AD是中线，点E是AD的中点，过A点作BC的平行线交CE的延长线于点F，连接BF．
BC，E，F分别是AB，AC的中点，以EF为直径的圆与BC的位置关系是（ ）