题目内容
4．
二次函数y=ax2+bx+c（a≠0）的图象如图所示，则下列关系式不正确的是（ ）| A． | abc＜0 | B． | a+b+c＜0 | C． | 2a-b＞0 | D． | 4a-b+c＜0 |
分析 由抛物线的开口方向判断a与0的关系，由抛物线与y轴的交点判断c与0的关系，然后根据对称轴及抛物线与x轴交点情况进行推理，进而对所得结论进行判断．
解答 解：由函数图象可得各系数的关系：a＜0，b＜0，c＞0，
∵a＜0，b＜0，c＞0，
∴abc＜0，故A错误；
∵x=1时，y＜0，
∴a+b+c＜0，故B错误；
∵对称轴x=-$\frac{b}{2a}$=-1，
∴b=2a，
∴2a-b=0，故C正确；
∵x=-2时，y＜0，
∴4a-2b+c＜0，故C错误．
故选C．
点评 主要考查图象与二次函数系数之间的关系，二次函数y=ax2+bx+c系数符号由抛物线开口方向、对称轴、抛物线与y轴的交点抛物线与x轴交点的个数确定．
练习册系列答案
相关题目
△ABC在平面直角坐标系中的位置如图所示．
19．
已知抛物线y=-2x2+4x-1．
（1）该抛物线的对称轴是直线x=1，顶点坐标（1，1）；
（2）选取适当的数据填入下表，并在图中的直角坐标系内描点画出该抛物线的图象；
（3）若该抛物线上两点A（x1，y1），B（x2，y2）的横坐标满足
x1＜x2＜1，试比较y1与y2的大小．
已知抛物线y=-2x2+4x-1．（1）该抛物线的对称轴是直线x=1，顶点坐标（1，1）；
（2）选取适当的数据填入下表，并在图中的直角坐标系内描点画出该抛物线的图象；
| x | … | … | |||||
| y | … | … |
x1＜x2＜1，试比较y1与y2的大小．
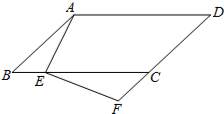如图，在?ABCD中，点E在BC边上，点F在DC的延长线上，且∠DAE=∠F．求证：BE•EC=FC•CD．