题目内容
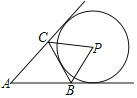
【题目】如图,在⊿![]() 中,以
中,以![]() 为直径的⊙
为直径的⊙![]() 与边
与边![]() 交于点
交于点![]() ,点
,点![]() 为⊙
为⊙![]() 上一点,连接
上一点,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,连接
,连接![]() .
.
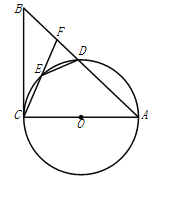
(1)若![]() ;求证:
;求证:![]() 是⊙
是⊙![]() 的切线;
的切线;
(2)若![]() .求⊙
.求⊙![]() 的直径.
的直径.
【答案】(1)证明见解析;(2)![]() 的直径为9
的直径为9
【解析】
(1)利用圆内接四边形对角互补以及邻补角的定义得出∠FED=∠A,进而得出∠B+∠A=90°,求出答案;
(2)利用相似三角形的判定与性质首先得出![]() ,进而求出即可.
,进而求出即可.![]()
(1)证明:∵∠A+∠DEC=180°,∠FED+∠DEC= 180°,
∴∠FED=∠A,
∵∠B+∠FED=90°
∴∠B+∠A=90°,
∴∠BCA=90°,
∴OC⊥BC,
∵OA为半径
∴BC是![]() 的切线
的切线
(2)解: ∵∠CFA=∠DFE,∠FED=∠A,
∴![]()
∴![]()
∴![]()
解得:AC=9,
即![]() 的直径为9
的直径为9

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】焦作市教育局为调查全市教师的运动情况,结合现今流行的“微信运动”,随机调查了本市![]() 名老师某日“微信运动”中的步数情况进行统计整理,绘制了如下的统计图表:
名老师某日“微信运动”中的步数情况进行统计整理,绘制了如下的统计图表:
步数 | 频数 | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
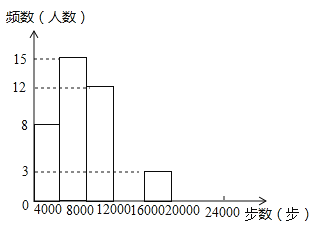
请根据以上信息,解答下列问题:
(1)写出![]() 的值,并补全频数分布直方图;
的值,并补全频数分布直方图;
(2)本市约有![]() 名教师,结合调查的数据估计日行走步数超过
名教师,结合调查的数据估计日行走步数超过![]() 步(包含
步(包含![]() 步)的教师有多少名?
步)的教师有多少名?
(3)若在被调查的教师中,选取日行走步数超过![]() 步(包含
步(包含![]() 步)的两名教师与大家分享心得,求被选取的两名教师恰好都在
步)的两名教师与大家分享心得,求被选取的两名教师恰好都在![]() 步(包含
步(包含![]() 步)以上的概率.
步)以上的概率.