题目内容
已知抛物线 与直线
与直线 相交于
相交于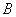 、
、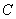 两点,且
两点,且 、
、 .
.
 (1)填空:
(1)填空: ,
, ;
;
(2)长度为 的线段
的线段 在线段
在线段 上移动,点
上移动,点
与点 在上述抛物线上,且线段
在上述抛物线上,且线段 与
与 始
始
终平行于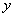 轴.
轴.
①连结 ,求四边形
,求四边形 的面积的最大值,
的面积的最大值,
并求出此时点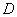 的坐标;
的坐标;
②在线段 移动的过程中,是否存在
移动的过程中,是否存在
 ?若存在,请直接写出此时点
?若存在,请直接写出此时点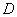 的
的
 坐标,若不存在,试说明理由.
坐标,若不存在,试说明理由.
(1)  ,
, ;……………………………………………………………4分
;……………………………………………………………4分
 (2) ①设直线
(2) ①设直线 的解析式为:
的解析式为: ,又过点
,又过点 、
、 ,
,
∴ ,解得:
,解得: ,
,
∴直线 的解析式为:
的解析式为: .……………………………………………………………7分
.……………………………………………………………7分
∵点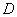 、
、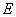 在直线
在直线 上,
上,
∴设 、
、 ,其中
,其中 ,如图,过点
,如图,过点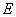 作
作 于点
于点 ,则
,则 ,
, ∥
∥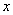 轴,则
轴,则
∴ ,
, ,
, ,
,
在 中,令
中,令 ,则
,则 ,由勾股定理得:
,由勾股定理得: ,即
,即 ,解得:
,解得: (舍去负值),则
(舍去负值),则 ,
, .
. ……………9分
……………9分
∵ ∥
∥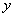 轴∥
轴∥ ,
,
∴ ,
,
∴ ,
,
 .
.
∴
把 代入上式,得:
代入上式,得:
 .当
.当 时,
时, 有最大值,最大值为
有最大值,最大值为 .
.
∴此时点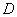 的坐标为
的坐标为
②符合条件的点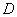 的坐标为
的坐标为 或
或 .
.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
 ,则
,则 D.若多项式
D.若多项式 是四次二项式,则
是四次二项式,则 2
2 点,BE=AD,AE=8,现有甲乙二人同时从E点出发,
点,BE=AD,AE=8,现有甲乙二人同时从E点出发, 倍,
倍, ∥
∥ ,直线
,直线 与直线
与直线 ,则
,则 °.
°.
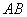 ∥
∥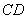 ,
,  上,且
上,且 .
. 求证:
求证: ≌
≌ .
. 的数是__________.
的数是__________. +
+ +
+ +…
+… 的值.
的值.