题目内容
如图,把矩形ABCD对折,设折痕为MN,再把B点叠在折痕上,得到Rt△ABE,沿着EB线折叠得到△AEF,若矩形的宽CD=4,△AEF的面积

- A.
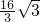
- B.

- C.

- D.

A
分析:首先根据平行线等分线段定理得到BE=BF,再结合AB⊥EF得到AE=AF.只需再进一步得到有一个角是60度即可.根据折叠知∠B′AE=∠BAE,根据等腰三角形的三线合一得到∠BAE=∠BAF,从而得到∠EAF=60°,根据有一个角是60°的等腰三角形是等边三角形,进而求出面积即可.
解答: 解:∵AD∥MN∥BC,AM=BM,
解:∵AD∥MN∥BC,AM=BM,
∴BE=BF,
又∠ABE=∠B′=90°,
∴AE=AF,
∴∠BAE=∠BAF.
根据折叠得∠B′AE=∠BAE,
∴∠B′AE=∠BAE=∠BAF=30°,
∴∠EAF=60°,
∴△EAF即为等边三角形.
∵矩形的宽CD=4,
∴AB=4,
tan30°= ,
,
即: =
= ,
,
解得:BF= ,
,
∴EF= ,
,
故△AEF的面积为: AB×EF=
AB×EF= ×4×
×4× =
=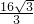 ,
,
故选:A.
点评:此题主要考查了翻折变换的性质、等边三角形的判定方法,平行线等分线段定理、线段垂直平分线的性质、等腰三角形的性质等知识点,得出△EAF即为等边三角形是解题关键.
分析:首先根据平行线等分线段定理得到BE=BF,再结合AB⊥EF得到AE=AF.只需再进一步得到有一个角是60度即可.根据折叠知∠B′AE=∠BAE,根据等腰三角形的三线合一得到∠BAE=∠BAF,从而得到∠EAF=60°,根据有一个角是60°的等腰三角形是等边三角形,进而求出面积即可.
解答:
 解:∵AD∥MN∥BC,AM=BM,
解:∵AD∥MN∥BC,AM=BM,∴BE=BF,
又∠ABE=∠B′=90°,
∴AE=AF,
∴∠BAE=∠BAF.
根据折叠得∠B′AE=∠BAE,
∴∠B′AE=∠BAE=∠BAF=30°,
∴∠EAF=60°,
∴△EAF即为等边三角形.
∵矩形的宽CD=4,
∴AB=4,
tan30°=
 ,
,即:
 =
= ,
,解得:BF=
 ,
,∴EF=
 ,
,故△AEF的面积为:
 AB×EF=
AB×EF= ×4×
×4× =
=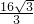 ,
,故选:A.
点评:此题主要考查了翻折变换的性质、等边三角形的判定方法,平行线等分线段定理、线段垂直平分线的性质、等腰三角形的性质等知识点,得出△EAF即为等边三角形是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,把矩形ABCD沿直线EF折叠,使点C与A重合.
如图,把矩形ABCD沿直线EF折叠,使点C与A重合. 24、如图,把矩形ABCD沿对角线BD对折,使点C落在点C′处,试证明AE=C′E.
24、如图,把矩形ABCD沿对角线BD对折,使点C落在点C′处,试证明AE=C′E. (2013•梧州)如图,把矩形ABCD沿直线EF折叠,若∠1=20°,则∠2=( )
(2013•梧州)如图,把矩形ABCD沿直线EF折叠,若∠1=20°,则∠2=( ) 如图,把矩形ABCD沿EF折叠,使点A与点C重叠.AB=8,BC=16,求DF的长.
如图,把矩形ABCD沿EF折叠,使点A与点C重叠.AB=8,BC=16,求DF的长. 如图,把矩形ABCD沿EF折叠,若∠1=50°,则∠AEF等于
如图,把矩形ABCD沿EF折叠,若∠1=50°,则∠AEF等于