Question

5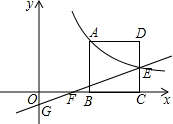．如图，正方形ABCD的顶点B、C在x轴的正半轴上，反比例函数y=$\frac{k}{x}$（k≠0）在第一象限的图象经过顶点A（a，4）和CD边上的点E（b，2），过点E的直线l交x轴于点F，交y轴于点G（0，-1），则△OFG的面积是（　　）

• A． $\frac{4}{3}$
• B． $\frac{5}{3}$
• C． $\frac{2}{3}$
• D． $\frac{7}{3}$

Answer 1

分析 由A（a，4）得到正方形的边长为2，则BC=2，所以n=2+m，根据反比例函数图象上点的坐标特征得到k=4•a=2（4+a），解得a=4，则E点坐标为（8，2），然后利用待定系数法确定直线GF的解析式为y=$\frac{1}{2}$x-1，再求y=0时对应自变量的值，从而得到点F的坐标，然后根据三角形面积公式求得即可．

解答 解：∵正方形的顶点A（a，4），
∴正方形的边长为4，
∴BC=4，
而点E（b，2），
∴b=4+a，即E点坐标为（4+a，2），
∴k=4•a=2（4+a），解得a=4，
∴E点坐标为（8，2），
设直线GF的解析式为y=mx+n，
把E（8，3），G（0，-1）代入得$\left\{\begin{array}{l}{8m+n=2}\\{n=-1}\end{array}\right.$，解得$\left\{\begin{array}{l}{m=\frac{3}{8}}\\{n=-1}\end{array}\right.$，
∴直线GF的解析式为y=$\frac{3}{8}$x-1，
当y=0时，$\frac{3}{8}$x-1=0，解得x=$\frac{8}{3}$，
∴点F的坐标为（$\frac{8}{3}$，0），
∴S_△OFG=$\frac{1}{2}$OF•OG=$\frac{1}{2}$×$\frac{8}{3}$×1=$\frac{4}{3}$．
故选A．

点评 本题考查了反比例函数与一次函数的交点问题：反比例函数与一次函数图象的交点坐标满足两函数解析式．也考查了待定系数法求函数解析式．