题目内容
(2011•温州一模)如图1,矩形ABCD中,AB=21,AD=12,E是CD边上的一点,DE=16,M是BC边上的中点,动点P从点A出发,沿边AB以每秒1单位长度的速度向终点B运动.设动点P的运动时间是t秒;
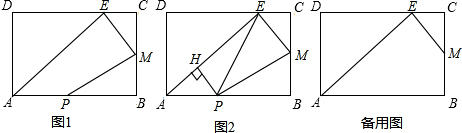
(1)求线段AE的长;
(2)当△ADE与△PBM相似时,求t的值;
(3)如图2,连接EP,过点P作PH⊥AE于H.
①当EP平分四边形PMEH的面积时,求t的值;
②以PE为对称轴作线段BC的轴对称图形B′C′,当线段B′C′与线段AE有公共点时,写出t的取值范围(直接写出答案).

(1)求线段AE的长;
(2)当△ADE与△PBM相似时,求t的值;
(3)如图2,连接EP,过点P作PH⊥AE于H.
①当EP平分四边形PMEH的面积时,求t的值;
②以PE为对称轴作线段BC的轴对称图形B′C′,当线段B′C′与线段AE有公共点时,写出t的取值范围(直接写出答案).
分析:(1)根据ABCD是矩形,得出∠D=90°,再由勾股定理即可求出AE的值;
(2)根据已知∠D=∠B=90°,即可求出△ADE与△PBM相似时,再分两种情况进行讨论;当∠DAE=∠PMB时有
=
,
解出t的值和当∠DAE=∠MPB时有
=
得出t的值;
(3)①根据题意得出S△EHP=S△EMP,求出t的两个值,再根据t的取值范围即可求出t的值;②根据PE为对称轴作线段BC的轴对称图形B′C′直接写出t的取值范围即可;
(2)根据已知∠D=∠B=90°,即可求出△ADE与△PBM相似时,再分两种情况进行讨论;当∠DAE=∠PMB时有
| DE |
| PB |
| AD |
| BM |
解出t的值和当∠DAE=∠MPB时有
| DE |
| BM |
| AD |
| PB |
(3)①根据题意得出S△EHP=S△EMP,求出t的两个值,再根据t的取值范围即可求出t的值;②根据PE为对称轴作线段BC的轴对称图形B′C′直接写出t的取值范围即可;
解答:解:(1)∵ABCD是矩形,
∴∠D=90°,
∴AE2=AD2+DE2,
∵AD=12,DE=16,
∴AE=20,
(2)∵∠D=∠B=90°,
∴△ADE与△PBM相似时,有两种可能;
当∠DAE=∠PMB时,有
=
,即
=
,
解得:t=13;
当∠DAE=∠MPB时,有
=
,即
=
,
解得t=
;
(3)①∵△ADE∽△PHA,
∴
=
=
,
∴
=
=
,
∴PH=
t,HA=
t,
∵S△EHP=S△EMP,
∴
×
t×(20-
t)=
×12×(5+21-t)-
×6×(21-t)-
×6×5,
解得:t=
,
∵0<t<21,
∴t=
;
②根据题意得:
≤t≤20.
∴∠D=90°,
∴AE2=AD2+DE2,
∵AD=12,DE=16,
∴AE=20,
(2)∵∠D=∠B=90°,
∴△ADE与△PBM相似时,有两种可能;
当∠DAE=∠PMB时,有
| DE |
| PB |
| AD |
| BM |
| 16 |
| 21-t |
| 12 |
| 6 |
解得:t=13;
当∠DAE=∠MPB时,有
| DE |
| BM |
| AD |
| PB |
| 16 |
| 6 |
| 12 |
| 21-t |
解得t=
| 33 |
| 2 |
(3)①∵△ADE∽△PHA,
∴
| AE |
| PA |
| AD |
| PH |
| DE |
| HA |
∴
| 20 |
| t |
| 12 |
| PH |
| 16 |
| HA |
∴PH=
| 3 |
| 5 |
| 4 |
| 5 |
∵S△EHP=S△EMP,
∴
| 1 |
| 2 |
| 3 |
| 5 |
| 4 |
| 5 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解得:t=
75±5
| ||
| 4 |
∵0<t<21,
∴t=
75-5
| ||
| 4 |
②根据题意得:
| 140 |
| 11 |
点评:此题考查了相似三角形的判定与性质;解题的关键是根据勾股定理、相似三角形的判定和性质的综合应用,要注意的是(2)中,有两种情况进行分类求解.

练习册系列答案
相关题目
 (2011•温州一模)由两个不同的长方体木块搭成的简易木凳如图所示,则它的主视图是( )
(2011•温州一模)由两个不同的长方体木块搭成的简易木凳如图所示,则它的主视图是( ) (2011•温州一模)如图,在纸上画出两个外离的圆,它们的半径分别为3cm和5cm,则圆心距可能是( )
(2011•温州一模)如图,在纸上画出两个外离的圆,它们的半径分别为3cm和5cm,则圆心距可能是( ) (2011•温州一模)如图,直角坐标系中,Rt△AOB的顶点A在x轴上,∠B=90°,OA=5,OB=3,现将△AOB绕原点O按顺时针方向旋转,得到△DOC,且点C在x轴上,则点D的坐标是( )
(2011•温州一模)如图,直角坐标系中,Rt△AOB的顶点A在x轴上,∠B=90°,OA=5,OB=3,现将△AOB绕原点O按顺时针方向旋转,得到△DOC,且点C在x轴上,则点D的坐标是( ) (2011•温州一模)如图,AB是⊙O的弦,C是
(2011•温州一模)如图,AB是⊙O的弦,C是