Question

△ABC中，BD，CD分别平分∠ABC和∠ACB，且交于点D，若∠A=50°，则∠BDC=

 

度．

Answer 1

分析：根据题意画出图形，利用三角形内角和为180°，以及角平分线的性质即可解答．

解答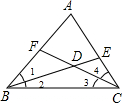：解：如图：在△ABC中，∠A+∠1+∠2+∠3+∠4=180°，
∵BD，CD分别平分∠ABC和∠ACB，
∴∠1=∠2，∠3=∠4，
∴2∠2+2∠3+∠A=180°，
∵∠A=50°，
∴∠2+∠3=

180°-∠A

2

=

180°-50°

2

=75°，
在△BDC中，∠BDC=180°-∠2-∠3=180°-75°=115°．

点评：三角形外角与内角的关系：三角形的一个外角等于和它不相邻的两个内角的和．