题目内容
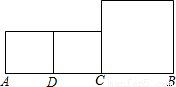
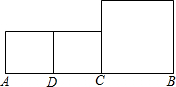如图线段AB=6，点C是AB上一点，点D是AC的中点，分别以AD，DC，CB为边作正方形，则AC=________时，三个正方形的面积之和最小．
4
分析：设AC为未知数，用二次函数表示出三个正方形的面积和，根据二次函数的最值问题的求法可得AC的值．
解答：设AC为x，三个正方形的面积和为y．则BC=6-x，AD=CD=
，
∴y=2×（）2+（6-x）2=
x2-12x+36，
∴x=-
=4时，三个正方形的面积之和最小．
故答案为4．
点评：考查二次函数的应用；设所求的数值为x，利用二次函数的最值问题进行求解是解决本题的基本思路．
分析：设AC为未知数，用二次函数表示出三个正方形的面积和，根据二次函数的最值问题的求法可得AC的值．
解答：设AC为x，三个正方形的面积和为y．则BC=6-x，AD=CD=
，∴y=2×（
）2+（6-x）2=x2-12x+36，∴x=-
=4时，三个正方形的面积之和最小．故答案为4．
点评：考查二次函数的应用；设所求的数值为x，利用二次函数的最值问题进行求解是解决本题的基本思路．
练习册系列答案
相关题目
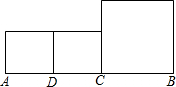（2012•郑州模拟）如图线段AB=6，点C是AB上一点，点D是AC的中点，分别以AD，DC，CB为边作正方形，则AC=