题目内容
在?ABCD中,AC与BD相交于点O,∠AOB=45°,BD=2,将△ABC沿直线AC翻折后,点B落在点B′处,那么DB′的长为分析:利用折叠的性质,即全等的性质可得AOB′=45°,所以∠BOB′=∠DOB′=90°,再解直角三角形即可.
解答:解:已知折叠就是已知图形的全等,
所以△ABC≌△AB′C,
则OB=OB′=
BD=1,
因为∠AOB=45°,
则AOB′=45°,
所以∠BOB′=∠DOB′=90°,
在Rt△DOB′中,OD=OB′=1,
利用勾股定理解得DB′=
.
故填
.
所以△ABC≌△AB′C,
则OB=OB′=
| 1 |
| 2 |
因为∠AOB=45°,
则AOB′=45°,
所以∠BOB′=∠DOB′=90°,
在Rt△DOB′中,OD=OB′=1,
利用勾股定理解得DB′=
| 2 |
故填
| 2 |
点评:已知折叠问题就是已知图形的全等,折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,只是位置变化.勾股定理也是解题的关键.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
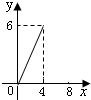
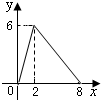
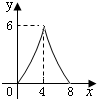
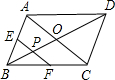 如图,在?ABCD中,AC=6,BD=8,P是对角线BD上的任意一点,过点P作EF∥AC,与?ABCD的两条边分别交于点E,F.设BP=x,EF=y,则下面能大致反映y与x之间关系的图象为( )
如图,在?ABCD中,AC=6,BD=8,P是对角线BD上的任意一点,过点P作EF∥AC,与?ABCD的两条边分别交于点E,F.设BP=x,EF=y,则下面能大致反映y与x之间关系的图象为( )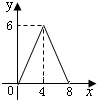
 如图,在?ABCD中,AC、BD相交于点O,点E是AB的中点,OE=5cm,则AD的长是
如图,在?ABCD中,AC、BD相交于点O,点E是AB的中点,OE=5cm,则AD的长是 如图,在?ABCD中,AC为对角线,BE⊥AC,DF⊥AC,E、F为垂足,求证:BE=DF.
如图,在?ABCD中,AC为对角线,BE⊥AC,DF⊥AC,E、F为垂足,求证:BE=DF.