题目内容
已知Rt△ABC中,∠C=90°,AC=3,BC=4,以C为圆心,r为半径的圆与边AB有两个交点,则r的取值范围是( )
A、r=
| ||
B、r>
| ||
| C、3<r<4 | ||
D、
|
考点:直线与圆的位置关系
专题:
分析:要使圆与斜边AB有两个交点,则应满足直线和圆相交,且半径不大于AC.要保证相交,只需求得相切时,圆心到斜边的距离,即斜边上的高即可.
解答: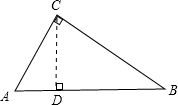 解:如图,
解:如图,
∵BC>AC,
∴以C为圆心,R为半径所作的圆与斜边AB有两个交点,则圆的半径应大于CD,小于或等于AC,
由勾股定理知,AB=
=5.
∵S△ABC=
AC•BC=
CD•AB=
×3×4=
×5•CD,
∴CD=
,
即R的取值范围是
<r≤3.
故选D.
 解:如图,
解:如图,∵BC>AC,
∴以C为圆心,R为半径所作的圆与斜边AB有两个交点,则圆的半径应大于CD,小于或等于AC,
由勾股定理知,AB=
| AC2+BC2 |
∵S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴CD=
| 12 |
| 5 |
即R的取值范围是
| 12 |
| 5 |
故选D.
点评:本题利用了勾股定理和垂线段最短的定理,以及直角三角形的面积公式求解.特别注意:圆与斜边有两个交点,即两个交点都应在斜边上.

练习册系列答案
相关题目
 如图是正方体的一种平面展开图,它的每个面上都有一个汉字,那么在原正方体的表面上,与汉字“之”相对的面上的汉字是
如图是正方体的一种平面展开图,它的每个面上都有一个汉字,那么在原正方体的表面上,与汉字“之”相对的面上的汉字是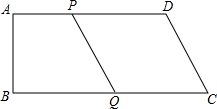 如图,梯形ABCD中,AD∥BC,AB⊥BC,点P从A出发以1厘米/秒的速度沿AD移动,点Q同时从C出发以2厘米/秒的速度沿CB移动,若AD=18厘米,BC=24厘米.求:
如图,梯形ABCD中,AD∥BC,AB⊥BC,点P从A出发以1厘米/秒的速度沿AD移动,点Q同时从C出发以2厘米/秒的速度沿CB移动,若AD=18厘米,BC=24厘米.求: