题目内容
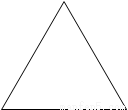
请你用3种不同的分割方法,将下列3个等边三角形分别分割成4个等腰三角形(在图中画出分割线,并且标出必要的角的度数)


练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
题目内容
请你用3种不同的分割方法,将下列3个等边三角形分别分割成4个等腰三角形(在图中画出分割线,并且标出必要的角的度数)



 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案