��Ŀ����
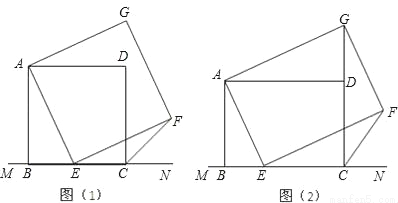
��ͼ��1������֪������ABCD��ֱ��MN���Ϸ���BC��ֱ��MN�ϣ�E��BC��һ�㣬��AEΪ����ֱ��MN���Ϸ���������AEFG��
��1������GD����֤����ADG�ա�ABE��
��2������FC���۲첢�²��FCN�Ķ�������˵�����ɣ�
��3����ͼ��2������ͼ��1����������ABCD��Ϊ����ABCD��AB=a��BC=b��a��bΪ��������E���߶�BC��һ���㣨�����˵�B��C������AEΪ����ֱ��MN���Ϸ�������AEFG��ʹ����Gǡ����������CD�ϣ��жϵ���E��B��C�˶�ʱ����FCN�Ĵ�С�Ƿ��ܱ��ֲ��䣿����FCN�Ĵ�С���䣬���ú�a��b�Ĵ���ʽ��ʾtan��FCN��ֵ������FCN�Ĵ�С�����ı䣬�����˵����
��ϰ��ϵ�д�
�����Ŀ


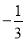 C.
C. 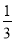 D. 3
D. 3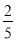 �����������зŽ�3�ź�ɫ���ӣ�ȡ�ð�ɫ���ӵĸ��ʱ�Ϊ
�����������зŽ�3�ź�ɫ���ӣ�ȡ�ð�ɫ���ӵĸ��ʱ�Ϊ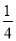 ����ԭ�������а�ɫ���ӣ�������
����ԭ�������а�ɫ���ӣ������� ���������Ľ⼯�������ϱ�ʾ������
���������Ľ⼯�������ϱ�ʾ������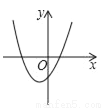 B.
B. 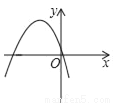 C.
C. 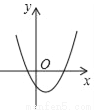 D.
D.