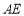Question

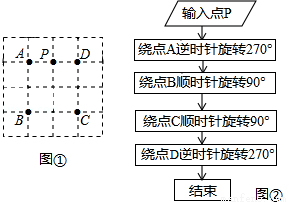
如图①，直角三角形AOB中，∠AOB=90°，AB平行于x轴，OA=2OB，AB=5，反比例函数 的图象经过点A．

（1）直接写出反比例函数的解析式；

（2）如图②，P（x，y）在（1）中的反比例函数图象上，其中1＜x＜8，连接OP，过O 作OQ⊥OP，且OP=2OQ，连接PQ．设Q坐标为（m，n），其中m＜0，n＞0，求n与m的函数解析式，并直接写出自变量m的取值范围；

（3）在（2）的条件下，若Q坐标为（m，1），求△POQ的面积．

 

 

Answer 1

【解析】

试题分析：（1）如图①，在Rt△OAB中利用勾股定理计算出OB=，OA=2，由于AB平行于x轴，则OC⊥AB，则可利用面积法计算出OC=2，在Rt△AOC中，根据勾股定理可计算出AC=4，得到A点坐标为（4，2），然后利用待定系数法确定反比例函数解析式为y=；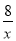

（2）分别过P、Q做x轴垂线，垂足分别为D、H，如图②，先证明Rt△POH∽Rt△OQD，根据相似的性质得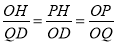，由于OP=2OQ，PH=y，OH=x，OD=﹣m，QD=n，则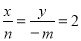，即有x=2n，y=﹣2m，而x、y满足y=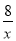，则2n•（﹣2m）=8，即mn=﹣2，当1＜x＜8时，1＜y＜8，所以1＜﹣2m＜8，解得﹣4＜m＜﹣；

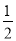（3）由于n=1时，m=﹣2，即Q点坐标为（﹣2，1），利用两点的距离公式计算出OQ=，则OP=2OQ=2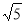，然后根据三角形面积公式求解．

试题解析：（1）如图①，

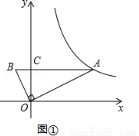
∵∠AOB=90°，

∴OA2+OB2=AB2，

∵OA=2OB，AB=5，

∴4OB2+OB2=25，解得OB=，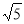

∴OA=2，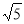

∵AB平行于x轴，

∴OC⊥AB，

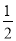∴OC•AB=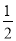OB•OA，即OC=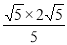=2，

在Rt△AOC中，AC=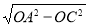=4，

∴A点坐标为（4，2），

设过A点的反比例函数解析式为y=，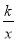

∴k=4×2=8，

∴反比例函数解析式为y=；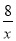

（2）分别过P、Q作x轴垂线，垂足分别为D、H，如图②，

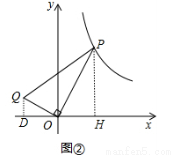
∵OQ⊥OP，

∴∠POH+∠QOD=90°，

∵∠POH+∠OPH=90°，

∴∠QOD=∠OPH，

∴Rt△POH∽Rt△OQD，

∴，

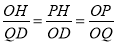∵P（x，y）在（1）中的反比例函数图象上，其中1＜x＜8，Q点点坐标为（m，n），其中m＜0，n＞0，OP=2OQ，

∴PH=y，OH=x，OD=﹣m，QD=n，

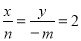∴，解得x=2n，y=﹣2m，

∵y=，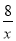

∴2n•（﹣2m）=8，

∴mn=﹣2（﹣4＜m＜﹣）；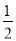

（3）∵n=1时，m=﹣2，即Q点坐标为（﹣2，1），

∴OQ=，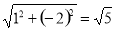

∴OP=2OQ=2，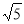

∴S△POQ=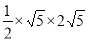=5．

考点：1、待定系数法；2、坐标与图形的性质；3、相似三角形的判定与性质；4、勾股定理