题目内容
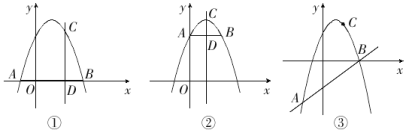
【题目】在平面直角坐标系中，直线AB与抛物线y=ax2+bx+c交于A，B(点A在点B的左侧)两点，点C是该抛物线上任意一点，过C点作平行于y轴的直线交AB于D，分别过点A，B作直线CD的垂线，垂足分别为点E，F．
特例感悟：
（1）已知：a=-2，b=4，c=6．
①如图①，当点C的横坐标为2，直线AB与x轴重合时，CD=____，|a|·AE·BF=___．
②如图②，当点C的横坐标为1，直线AB//x轴且过抛物线与y轴的交点时，CD=_____，|a|·AE·BF=_______．
③如图③，当点C的横坐标为2，直线AB的解析式为y=x-3时，CD=___，|a|·AE·BF=___．
猜想论证：
（2）由（1）中三种情况的结果，请你猜想在一般情况下CD与|a|·AE·BF之间的数量关系，并证明你的猜想．拓展应用．
（3）若a=-1，点A，B的横坐标分别为-4，2，点C在直线AB的上方的抛物线上运动(点C不与点A，B重合)，在点C的运动过程中，利用（2）中的结论求出△ACB的最大面积．
【答案】（1）①6，6；②2，2；③7，7；（2）
，见解析；（3）27
【解析】
(1)①求得点A、B、C的坐标，得到点E、D、F三点重合，即可求得CD的长以及|a|·AE·BF的值；
②求得点A、B、C的坐标，得到点E、D、F三点重合，即可求得CD的长以及|a|·AE·BF的值；
③解方程组求得点A、B的坐标，再求得点C、D的坐标，即可求得CD的长以及|a|·AE·BF的值；
(2)利用参数法，设A、B、C三横坐标分别为：
，直线AB的解析式为
，根据一元二次方程根与的关系，求得|a|·AE·BF
，再利用两点之间距离公式求得CD，即可证明；
(3)设点C的横坐标为
，△ACB的面积为S，根据
，点A，B的横坐标分别为-4，2，得到
，
，
，利用三角形面积公式即可得到关于x的二次函数，利用二次函数的最值即可求解．
(1)已知：
，则抛物线的解析式为
，
①令
，则
或
,
∴点A、B的坐标分别为
，
∵点C的横坐标为2，
∴点C的坐标为
∵直线AB与x轴重合，
∴点E、D、F三点重合，
如图：
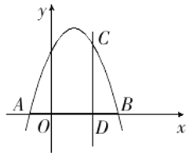
∴CD=6，
|a|·AE·BF=
；
②令
，则
,
∴点A的坐标为
抛物线的对称轴为
，
∵直线AB//x轴，
∴点B的坐标分别为
∵点C的横坐标为1，
∴点C的坐标为
∵直线AB//x轴，
∴点E、D、F三点重合，
如图：
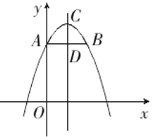
∴CD=8-6=2，
|a|·AE·BF=
；
③解方程组
得：
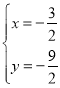或
，
∴点A、B的坐标分别为
，
∵点C的横坐标为2，
∴点C的坐标为
∵直线CD平行于y轴，
∴点D的横坐标为2，
把
代入
得：
，
∴点D的坐标为
如图：
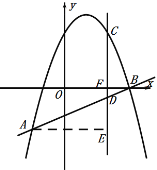
∴CD=CF-FD=6+1=7，
|a|·AE·BF=
；
(2)数量关系为：，
理由如下：
设A、B、C三横坐标分别为：，直线AB的解析式为，
联立方方程和
，消去
并整理得：
，
∵
是方程的两根，
∴
，
，
则
，
，
∴
·AE·BF=
，
又∵点C的横坐标为t，
∴点C的坐标为
∵直线CD平行于y轴，
∴点D的横坐标为t，
把
代入得：
，
∴点D的坐标为
∴CD=
=
，
∴CD=·AE·BF；
(2)设点C的横坐标为，△ACB的面积为S，
过点C作CD平行于y轴交AB于D，
∵点A、B的横坐标分别为-4、2，
则，，
∵，点A，B的横坐标分别为-4，2，
则抛物线的解析式为
，
∴点A、B的坐标分别为
，
设直线AB的解析式为
，则
，
解得：
，
∴直线AB的解析式为
，
∴点C的坐标为
点D的坐标为
∴
，
∵
，
由于
，
∴当时，
．
