题目内容

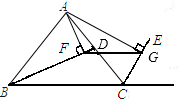
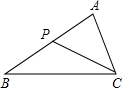精英家教网如图，若P为△ABC的边AB上一点（AB＞AC），则下列条件不一定能保证△ACP∽△ABC的有（　　）
A、∠ACP=∠B
B、∠APC=∠ACB
C、
AC
AB
=
AP
AC
D、
PC
BC
=
AC
AB
分析：根据相似三角形的判定方法．利用公共角∠A进行求解．
解答：解：∵∠A=∠A，
∴当∠APC=∠ACB或∠ACP=∠B或AC：AB=AP：AC或AC2=AB•AP时，
△ACP∽△ABC．
故选D．
点评：此题考查了相似三角形的判定：
①有两个对应角相等的三角形相似；
②有两个对应边的比相等，且其夹角相等，则两个三角形相似；
③三组对应边的比相等，则两个三角形相似．
练习册系列答案
相关题目
（1）如图，已知△ABC中，O为∠ABC和∠ACB的平分线BO，CO的交点．试猜想∠BOC和∠A的关系，并说明理由；
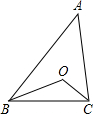
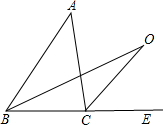
精英家教网
（2）如图，若O为∠ABC和∠ACB外角的平分线BO，CO的交点，则∠BOC与∠A的关系又该怎样？为什么？
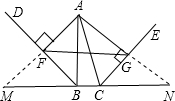
精英家教网
（1）如图所示，BD，CE分别是△ABC的外角平分线，过点A作AF⊥BD，AG⊥CE，垂足分别为F，G，连接FG，延长AF，AG，与直线BC分别交于点M、N，那么线段FG与△ABC的周长之间存在的数量关系是什么？
即：FG=
 
（AB+BC+AC）
（直接写出结果即可）
精英家教网
（2）如图，若BD，CE分别是△ABC的内角平分线；其他条件不变，线段FG与△ABC三边之间又有怎样的数量关系？请写出你的猜想，并给予证明．
精英家教网
（3）如图，若BD为△ABC的内角平分线，CE为△ABC的外角平分线，其他条件不变，线段FG与△ABC三边又有怎样的数量关系？直接写出你的猜想即可．不需要证明．答：线段FG与△ABC三边之间数量关系是
 
．
精英家教网
精英家教网如图，若P为△ABC的边AB上一点（AB＞AC），则下列条件能保证△ACP∽△ABC的有（　　）
①∠ACP=∠B；②∠APC=∠ACB；③
AC
AB
=
AP
AC
；④
PC
BC
=
AC
AB
．
A、①②B、①②③④
C、①②④D、①②③
如图，若D为△ABC的边AC上一点，且AB=AC，AD=BD=BC，则∠A=
36°
36°
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网