题目内容
如图,一次函数的图象与反比例函数的图象相交于A、B两点。
(1)利用图中的条件,求反比例函数和一次函数的表达式;
(2)根据图象写出使一次函数的值大于反比例函数的值的 的取值范围;
的取值范围;
(3)求△ABO的面积。
(1)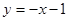 ,
,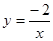 ;(2)
;(2)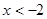 或
或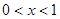 ;(3)
;(3)
解析试题分析:(1)设反比例函数关系式为 ,再根据A点坐标即可求得k的值,从而可得到n的值,设一次函数关系式为
,再根据A点坐标即可求得k的值,从而可得到n的值,设一次函数关系式为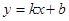 ,由A、B两点的坐标根据待定系数法即可求得结果;
,由A、B两点的坐标根据待定系数法即可求得结果;
(2)找到一次函数的图象在反比例函数的图象上方的部分即可得到结果;
(3)把△ABO放在一个长方形中,用长方形的面积减去周围的小直角三角形的面积即可得到结果.
(1)设反比例函数关系式为
∵图象过点A(-2,1)
∴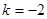
∴反比例函数关系式为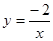
当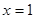 ,
,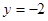
∴B点坐标为(1,-2)
设一次函数关系式为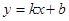
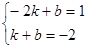 ,解得
,解得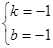
∴一次函数关系式为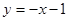 ;
;
(2)由图象可得,当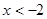 或
或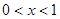 时,一次函数的值大于反比例函数的值;
时,一次函数的值大于反比例函数的值;
(3)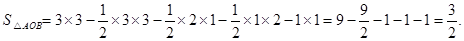
考点:反比例函数和一次函数的交点问题
点评:解答此类不规则三角形的面积一般是把这个三角形放在长方形中,用长方形的面积减去周围的小直角三角形的面积.

练习册系列答案
相关题目
 如图,已知反比例函数y=
如图,已知反比例函数y=
 解答:
解答:
