Question

【题目】如图，已知函数y=x+1的图象与y轴交于点A，一次函数y=kx+b的图象经过点B(0，-1)，与x轴以及y=x+1的图象分别交于点C、D，且点D的坐标为(1，n)，

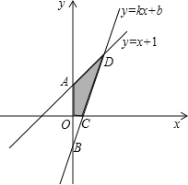
(1)求n，k ，b的值；

(2)若函数y=kx+b的函数值大于函数y=x+1的函数值，则x的取值范围是多少？

(3)求四边形AOCD的面积；

Answer 1

【答案】（1）n，k ，b的值分别为：2，3，-1；（2）x＞1（3）

【解析】

（1）对于直线y=x+1，令x=0求出y的值，确定出A的坐标，把B坐标代入y=kx+b中求出b的值，再将D坐标代入y=x+1求出n的值，进而将D坐标代入求出k的值即可；
（2）由两一次函数解析式，结合图象确定出x的范围即可；
（3）过D作DE垂直于x轴，如图1所示，四边形AOCD面积等于梯形AOED面积减去三角形CDE面积，求出即可；

解：（1）对于直线y=x+1，令x=0，得到y=1，即A（0，1），
把B（0，-1）代入y=kx+b中，得：b=-1，
把D（1，n）代入y=x+1得：n=2，即D（1，2），
把D坐标代入y=kx-1中得：2=k-1，即k=3，
故n，k ，b的值分别为：2，3，-1；
（2）∵一次函数y=x+1与y=3x-1交于D（1，2），
∴由图象得：函数y=kx+b的函数值大于函数y=x+1的函数值时x的取值范围是x＞1；
故答案为：x＞1；
（3）过D作DE⊥x轴，垂足为E，如图1所示，

则S四边形AOCD=S梯形AOED-S△CDE=（AO+DE）OE-CEDE=×（1+2）×1-××2=-=.