题目内容
如图，已知在△ABC中，∠C=90°，AD是角平分线，过点B作BA的垂线与AD的延长线相交于点E，求证：△BDE是等腰三角形．考点：等腰三角形的判定
专题：证明题
分析：在直角△ACD中根据直角三角形的两锐角互余可以证得∠ADC+∠DAC=90°，在直角△ABE中得到∠E+∠BAE=90°，根据等角的余角相等即可证得∠E=∠BDE，利用等角对等边即可证得．
解答：证明：∵在直角△ACD中，∠ADC+∠DAC=90°，
又∵∠BDE=∠ADC，
∴∠BDE+∠DAC=90°，
∵直角△ABE中，∠E+∠BAE=90°，
又∵AD是∠BAC的平分线，即∠BAE=∠DAC，
∴∠E=∠BDE，
∴BE=BD，即△BDE是等腰三角形．
又∵∠BDE=∠ADC，
∴∠BDE+∠DAC=90°，
∵直角△ABE中，∠E+∠BAE=90°，
又∵AD是∠BAC的平分线，即∠BAE=∠DAC，
∴∠E=∠BDE，
∴BE=BD，即△BDE是等腰三角形．
点评：本题考查了直角三角形的性质，以及等腰三角形的判定方法：等角对等边，证明同一个三角形中的两边相等的方法，常用方法是证明两边所对的角相等．
练习册系列答案
阅读快车系列答案
相关题目
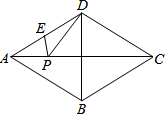已知四边形ABCD为菱形，∠BAD=60°，E为AD中点，AB=6cm，P为AC上任一点．求PE+PD的最小值是某同学在解方程3x-1=□x+2时，把□处的数字看错了，解得x=-1，则该同学把□看成了（ ）
| A、3 | ||
B、
| ||
| C、6 | ||
D、-
|
如图，点A，C和B都在⊙O上，且四边形ACBO为菱形，求证：点C是
如图，在?ABCD中，若BE平分∠ABC，求ED．