Question

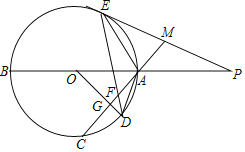
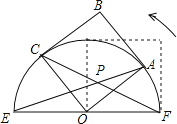
【题目】如图，正方形OABC的边长为2，以O为圆心，EF为直径的半圆经过点A，连接AE，CF相交于点P，将正方形OABC从OA与OF重合的位置开始，绕着点O逆时针旋转90°，交点P运动的路径长是_____．

Answer 1

【答案】

【解析】

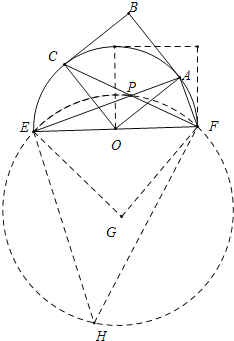
如图点P运动的路径是以G为圆心的弧，在⊙G上取一点H，连接EH、FH，只要证明∠EGF=90°，求出GE的长即可解决问题．

如图点P运动的路径是以G为圆心的弧，在⊙G上取一点H，连接EH、FH．

∵四边形AOCB是正方形，

∴∠AOC=90°，

∴∠AFP=∠AOC=45°，

∵EF是⊙O直径，

∴∠EAF=90°，

∴∠APF=∠AFP=45°，

∴∠EPF=135°，

∵EF是定值，

∴点P在以点G为圆心，GE为半径的圆上，

∴∠H=∠APF=45°，

∴∠EGF=2∠H=90°，

∵EF=4，GE=GF，

∴EG=GF=2，

∴的长==

故答案为．