题目内容
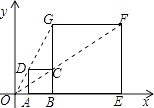
【题目】如图，在平面直角坐标系中，平行四边形
的边
在
轴上，点
，线段
，线段
，且
，
与
的交点记为
，连接
．
（1）求
的面积．
（2）如图2，在线段上有两个动点
、
（在点上方），且
，点
为
中点，点
为线段
上一动点，当
的值最小时，求出此时点的坐标；
（3）在（2）的条件下，在轴上找一点
，轴上找一点
，使得
取得最小值，请求出的最小值．
【答案】（1）
；（2）
，（3）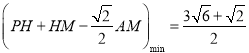
；
【解析】
（1）过点D作DP⊥AB于点P，则利用直角三角形的性质和勾股定理求出DP的长度，即可得到答案；
（2）根据题意，作点F关于BE的对称点H，过点H作HI∥BE，取HI=KG=
，过点I作y轴的平行线，交AB于点J，交BE于点K，交CD于点P，此时
得到最小值，由轴对称的性质，勾股定理，30度直角三角形的性质，求出BG的长度，然后求出BJ的长度，即可得到点P的坐标；
（3）如图，作点P关于y轴的对称点
，作
，交x轴于点M，交y轴于点H，则此时
最小；由等腰直角三角形的性质和勾股定理求出
的长度，然后求出AM的长度，即可求出最小值.
解：（1）如图，过点D作DP⊥AB于点P，
∵
，
∴
，
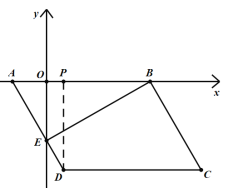
在Rt△ADP中，AD=6，
∴AP=3，
由勾股定理，得
，
∴
；
（2）如图，作点F关于BE的对称点H，过点H作HI∥BE，取HI=KG=，过点I作y轴的平行线，交AB于点J，交BE于点K，交CD于点P，此时得到最小值；
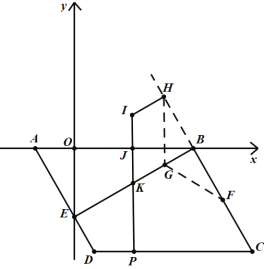
则四边形KGHI是平行四边形，
∴HG=IK=FG，HI=KG=，
在Rt△AOE中，∠OAE=60°，OA=2，
∴∠AEO=30°，
∴AE=2OA=4，
∴OE=
，
在Rt△OBE中，OB=6，
∴
，
∵
，
∴△ABE是直角三角形，即AE⊥BE，
∴∠ABE=30°，∠FBG=90°，
∴∠BGH=∠BGF=60°，
∴∠BFG=30°，
∴
，
∵点F为BC中点，
∴BF=3，
由勾股定理，得：
，
∴
，
∴
，
在Rt△BJK中，∠ABE=30°，
∴
，
∴
，
∴
，
∵
，
∴点P的坐标为：（3，
）；
（3）如图，作点P关于y轴的对称点，作，交x轴于点M，交y轴于点H，则此时最小；
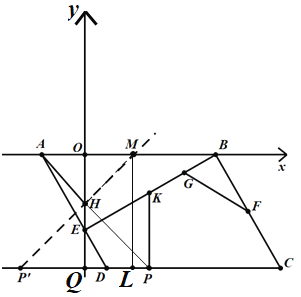
由轴对称的性质，得
，
∴
，
∵，
∴
是等腰直角三角形，
∴
；
∵AB∥CD，
∴四边形OMLQ是矩形，
∴OM=QL=
，
∴AM=
，
∴
，
∴的最小值为
.
