题目内容
(本题10分)等边⊿ABC的边长为6,点E、F分别是边AC、BC上的点,连结AF,BE相交于点P.
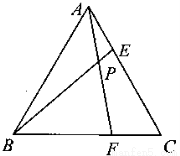
(1)若AE=CF: ①求∠APB的度数.(3分)②若AE=2,试求的 值.(3分)
值.(3分)
(2)若AF=BE,当点E从点A运动到点C时,试求点P经过的路径长.(4分)
(1)①120°;②12 ;(2) 或3
或3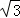 .
.
【解析】
试题分析:(1)①证明△ABE≌△CAF,借用外角即可得到答案;
②利用勾股定理求得AF的长度,再利用平行线分线段成比例定理或三角形相似的性质求得 ,即可得到答案;
,即可得到答案;
(2)当点F靠近点C的时候,点P的路径是一段弧,由题目不难看出当E为AC的中点的时候,点P经过弧AB的中点,此时△ABP为等腰三角形,继而求得半径和对应的圆心角的度数,求得答案,点F靠近点B时,点P的路径就是过点B向AC作的垂线段的长度.
试题解析:(1)①证明:∵△ABC为等边三角形,
∴AB=AC,∠C=∠CAB=60°,
在△ABE和△CAF中,
 ,
,
∴△ABE≌△CAF(SAS),
∴AF=BE,∠ABE=∠CAF.
又∵∠APE=∠BPF=∠ABP+∠BAP,
∴∠APE=∠BAP+∠CAF=60°.
∴∠APB=180°﹣∠APE=120°.
②∵∠C=∠APE=60°,∠PAE=∠CAF,
∴△APE∽△ACF,
∴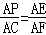 ,即
,即 ,所以APAF=12 ;
,所以APAF=12 ;
(2)若AF=BE,有AE=BF或AE=CF两种情况.
①当AE=CF时,点P的路径是一段弧,由题目不难看出当E为AC的中点的时候,点P经过弧AB的中点,此时△ABP为等腰三角形,且∠ABP=∠BAP=30°,
∴∠AOB=120°,又∵AB=6,
∴OA=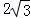 ,
,
点P的路径是 .
.
②当AE=BF时,点P的路径就是过点B向AC做的垂线段的长度;
∵等边三角形ABC的边长为6,∴点P的路径的长度为:  .
.
所以,点P经过的路径长为 或3
或3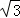 .
.

考点:等边三角形的性质;相似三角形的判定和性质;弧长公式.
考点分析: 考点1:三角形 (1)三角形的概念:由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形.组成三角形的线段叫做三角形的边.
相邻两边的公共端点叫做三角形的顶点.
相邻两边组成的角叫做三角形的内角,简称三角形的角.
(2)按边的相等关系分类:不等边三角形和等腰三角形(底和腰不等的等腰三角形、底和腰相等的等腰三角形即等边三角形).
(3)三角形的主要线段:角平分线、中线、高.
(4)三角形具有稳定性. 试题属性
- 题型:
- 难度:
- 考核:
- 年级:

 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案 与正比例函数
与正比例函数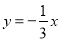 交于
交于 ,
, 两点,过点
两点,过点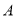 作
作 轴的平行线与过点
轴的平行线与过点 作
作 轴的平行线交于点C,则
轴的平行线交于点C,则 的面积为___________________.
的面积为___________________.
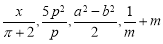 ,其中分式共有( ).
,其中分式共有( ).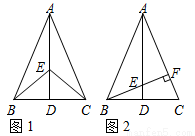
 = ;
= ; x2+xy+
x2+xy+