题目内容
(本题14分)如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB于点D.点P从点D出发,沿线段DC向点C运动,点Q从点C出发,沿线段CA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到C时,两点都停止.设运动时间为t秒.

(1)求线段CD的长;
(2)设△CPQ的面积为S,求S与t之间的函数关系式,并确定在运动过程中是否存在某一时刻t,使得S△CPQ:S△ABC=9:100?若存在,求出t的值;若不存在,说明理由.
(3)当t为何值时,△CPQ为等腰三角形?
(1)4.8;(2) ,存在,
,存在, 秒或
秒或 ;(3)2.4秒或
;(3)2.4秒或 秒或
秒或 秒.
秒.
【解析】
试题分析:(1)利用勾股定理可求出AB长,再用等积法就可求出线段CD的长.
(2)过点P作PH⊥AC,垂足为H,通过三角形相似即可用t的代数式表示PH,从而可以求出S与t之间的函数关系式;利用S△CPQ:S△ABC=9:100建立t的方程,解方程即可解决问题.
(3)可分三种情况进行讨论:由CQ=CP可建立关于t的方程,从而求出t;由PQ=PC或QC=QP不能直接得到关于t的方程,可借助于等腰三角形的三线合一及三角形相似,即可建立关于t的方程,从而求出t.
试题解析:(1)如图1,

∵∠ACB=90°,AC=8,BC=6,∴AB=10.
∵CD⊥AB,∴S△ABC= BCAC=
BCAC= ABCD.
ABCD.
∴CD= .
.
∴线段CD的长为4.8.
(2)①过点P作PH⊥AC,垂足为H,如图2所示.

由题可知DP=t,CQ=t.则CP=4.8﹣t.
∵∠ACB=∠CDB=90°,∴∠HCP=90°﹣∠DCB=∠B.
∵PH⊥AC,∴∠CHP=90°.∴∠CHP=∠ACB.∴△CHP∽△BCA.
∴ ,∴
,∴ ,∴PH=
,∴PH= .
.
∴S△CPQ= CQPH=
CQPH= .
.
②存在某一时刻t,使得S△CPQ:S△ABC=9:100.
∵S△ABC= ,且S△CPQ:S△ABC=9:100,
,且S△CPQ:S△ABC=9:100,
∴ ,整理得:
,整理得: ,即
,即 ,解得:
,解得: 或
或 .
.
∵ ,∴当
,∴当 或
或 秒时,S△CPQ:S△ABC=9:100.
秒时,S△CPQ:S△ABC=9:100.
(3)①若CQ=CP,如图1,则 ,解得:
,解得: .
.
②若PQ=PC,如图2所示.
∵PQ=PC,PH⊥QC,∴QH=CH= QC=
QC= .
.
∵△CHP∽△BCA,∴ .∴
.∴ .解得:
.解得: .
.
③若QC=QP,过点Q作QE⊥CP,垂足为E,如图3所示.
同理可得: .
.
综上所述:当t为2.4秒或 秒或
秒或 秒时,△CPQ为等腰三角形.
秒时,△CPQ为等腰三角形.

考点:1.相似形综合题;2.一元二次方程的应用;3.等腰三角形的性质.
考点分析: 考点1:一元二次方程 定义:只含有一个未知数,并且未知数的最高次数是2的整式方程叫做一元二次方程。
一元二次方程的一般形式:

它的特征是:等式左边是一个关于未知数x的二次多项式,等式右边是零,其中 ax2叫做二次项,a叫做二次项系数;bx叫做一次项,b叫做一次项系数;c叫做常数项。 考点2:图形的相似 形状相同,大小不同的两个图形相似 试题属性
- 题型:
- 难度:
- 考核:
- 年级:

 智能训练练测考系列答案
智能训练练测考系列答案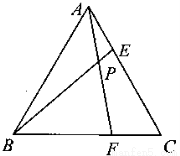
 值.(3分)
值.(3分) 的是 ( )
的是 ( )  B、
B、
 D、
D、


 B、
B、 C、
C、 D、
D、


 +
+ -
- )×48
)×48
 -60×
-60× +60×
+60× .
. =-a,则实数a在数轴上的对应点一定在 ( )
=-a,则实数a在数轴上的对应点一定在 ( )