题目内容
 如图,AB∥CD,EG、EM、FM分别平分∠AEF,∠BEF,∠EFD,则图中与∠DFM相等的角(不含它本身)的个数为
如图,AB∥CD,EG、EM、FM分别平分∠AEF,∠BEF,∠EFD,则图中与∠DFM相等的角(不含它本身)的个数为
- A.5
- B.6
- C.7
- D.8
C
分析:由FM平分∠EFD可知:与∠DFM相等的角有∠EFM;由于AB∥CD,EG、EM、FM分别平分∠AEF、∠BEF、∠EFD,根据平行线的性质和判定定理可以推导出FM∥EG,由此可以写出与∠DFM相等的角.
解答:∵FM平分∠EFD,
∴∠EFM=∠DFM= ∠CFE,
∠CFE,
∵EG平分∠AEF,
∴∠AEG=∠GEF= ∠AEF,
∠AEF,
∵EM平分∠BEF,
∴∠BEM=∠FEM= ∠BEF,
∠BEF,
∴∠GEF+∠FEM= (∠AEF+∠BEF)=90°,即∠GEM=90°,
(∠AEF+∠BEF)=90°,即∠GEM=90°,
∠FEM+∠EFM= (∠BEF+∠CFE),
(∠BEF+∠CFE),
∵AB∥CD,
∴∠EGF=∠AEG,∠CFE=∠AEF
∴∠FEM+∠EFM= (∠BEF+∠CFE)=
(∠BEF+∠CFE)= (BEF+∠AEF)=90°,
(BEF+∠AEF)=90°,
∴在△EMF中,∠EMF=90°,
∴∠GEM=∠EMF,
∴EG∥FM,
∴与∠DFM相等的角有:∠EFM、∠GEF、∠EGF、∠AEG以及∠GEF、∠EGF、∠AEG三个角的对顶角.
故选C.
点评:重点考查了角平分线的定义,平行线的性质和判定定理,推导较复杂.
分析:由FM平分∠EFD可知:与∠DFM相等的角有∠EFM;由于AB∥CD,EG、EM、FM分别平分∠AEF、∠BEF、∠EFD,根据平行线的性质和判定定理可以推导出FM∥EG,由此可以写出与∠DFM相等的角.
解答:∵FM平分∠EFD,
∴∠EFM=∠DFM=
 ∠CFE,
∠CFE,∵EG平分∠AEF,
∴∠AEG=∠GEF=
 ∠AEF,
∠AEF,∵EM平分∠BEF,
∴∠BEM=∠FEM=
 ∠BEF,
∠BEF,∴∠GEF+∠FEM=
 (∠AEF+∠BEF)=90°,即∠GEM=90°,
(∠AEF+∠BEF)=90°,即∠GEM=90°,∠FEM+∠EFM=
 (∠BEF+∠CFE),
(∠BEF+∠CFE),∵AB∥CD,
∴∠EGF=∠AEG,∠CFE=∠AEF
∴∠FEM+∠EFM=
 (∠BEF+∠CFE)=
(∠BEF+∠CFE)= (BEF+∠AEF)=90°,
(BEF+∠AEF)=90°,∴在△EMF中,∠EMF=90°,
∴∠GEM=∠EMF,
∴EG∥FM,
∴与∠DFM相等的角有:∠EFM、∠GEF、∠EGF、∠AEG以及∠GEF、∠EGF、∠AEG三个角的对顶角.
故选C.
点评:重点考查了角平分线的定义,平行线的性质和判定定理,推导较复杂.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目
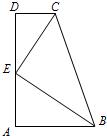 23、如图,AB∥CD,∠A=90°,AB=2,BC=3,CD=1,E是AD中点.求证:CE⊥BE.
23、如图,AB∥CD,∠A=90°,AB=2,BC=3,CD=1,E是AD中点.求证:CE⊥BE.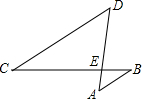 如图,AB∥CD,AD与BC相交于点E,如果AB=2,CD=6,AE=1,那么DE=
如图,AB∥CD,AD与BC相交于点E,如果AB=2,CD=6,AE=1,那么DE=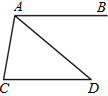 4、如图,AB∥CD,∠C=80°,∠CAD=60°,则∠BAD的度数等于( )
4、如图,AB∥CD,∠C=80°,∠CAD=60°,则∠BAD的度数等于( ) 34、如图,AB∥CD,P是BC上的一个动点,设∠CDP=∠1,∠CPD=∠2,请你猜想出∠1、∠2与∠B之间的关系,并说明理由.
34、如图,AB∥CD,P是BC上的一个动点,设∠CDP=∠1,∠CPD=∠2,请你猜想出∠1、∠2与∠B之间的关系,并说明理由. 如图,AB∥CD,∠1=58°,则∠2的度数是( )
如图,AB∥CD,∠1=58°,则∠2的度数是( )