题目内容
9.已知关于x的方程x2-ax+1=0有两个相等的实数根,且该实数根也是关于x的方程$\frac{2}{x+b}$=$\frac{1}{x-1}$的根,则ba的值为( )| A. | $\frac{1}{9}$ | B. | -$\frac{1}{9}$ | C. | 9 | D. | -9 |
分析 先根据判别式的意义得到△=a2-4=0,解得a=2或a=-2,再解x2-2x+1=0得x1=x2=1,解方程x2+2x-1=0得x1=x2=-1,由于方程的实数根是关于x的方程$\frac{2}{x+b}$=$\frac{1}{x-1}$的根,所以a=-2,然后x=-1代入$\frac{2}{x+b}$=$\frac{1}{x-1}$求得b=-3,然后利用负整数指数幂的意义计算ba.
解答 解:根据题意得△=a2-4=0,解得a=2或a=-2,
一元二次方程变形为x2-2x+1=0或x2+2x-1=0,
解x2-2x+1=0得x1=x2=1,解方程x2+2x-1=0得x1=x2=-1,
因为方程的实数根是关于x的方程$\frac{2}{x+b}$=$\frac{1}{x-1}$的根,
所以a=-2,
把x=-1代入$\frac{2}{x+b}$=$\frac{1}{x-1}$得$\frac{2}{-1+b}$=$\frac{1}{-1-1}$,解得b=-3,
所以ba=(-3)-2=$\frac{1}{9}$.
故选A.
点评 本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:当△>0时,方程有两个不相等的实数根;当△=0时,方程有两个相等的实数根;当△<0时,方程无实数根.

练习册系列答案
相关题目
3.一只蚂蚁沿着数轴从表示$\frac{1}{5}$的点爬到表示$\frac{4}{5}$的点,它经过的表示分数的点有( )
| A. | 0个 | B. | 2个 | C. | 4个 | D. | 无数个 |
20.已知平面直角坐标系内的一点P(2,-3),则点P到x轴的距离是( )
| A. | 2 | B. | -3 | C. | -2 | D. | 3 |
17.若(x+y)( )=x2-y2,其中括号内的是( )
| A. | -x-y | B. | -x+y | C. | x-y | D. | x+y |
4.根据两个图形中阴影部分的面积相等,可以验证( )
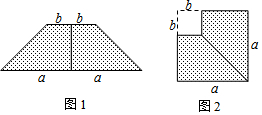

| A. | (a+b)(a-b)=a2-b2 | B. | (a-b)2=a2-2ab+b2 | ||
| C. | (a+b)2=a2+2ab+b2 | D. | (a+2b)(a-b)=a2+ab-2b2 |
14.如图所示,用直尺度量线段AB,可以读出AB的长度为( )


| A. | 6cm | B. | 7cm | C. | 8cm | D. | 9cm |
17.一个等腰三角形的两边分别为2,3,则这个三角形的周长为( )
| A. | 3+4 | B. | 6+2 | C. | 6+4 | D. | 3+4或6+2 |
18.如图,若有一个几何体的三视图如图所示,则这个几何体是( )


| A. | 三棱柱 | B. | 四棱柱 | C. | 五棱柱 | D. | 长方体 |