题目内容
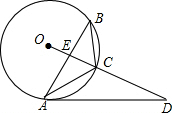 已知:如图,等腰△ABC内接于⊙O,点D在OC的延长线上,连接AD,交AB于点E,∠D=40°,∠B=25°.
已知:如图,等腰△ABC内接于⊙O,点D在OC的延长线上,连接AD,交AB于点E,∠D=40°,∠B=25°.(1)求证:AD是⊙O的切线;
(2)若⊙O的半径为5,求弦AB的长(结果精确到0.01).
分析:(1)连接OA,由于∠B=25°,利用圆周角定理可求∠O=50°,而∠D=40°,那么∠O+∠D=90°,利用三角形内角和等于180°,可求∠OAD=90°,即AD是⊙O的切线;
(2)由于AC=BC,那么
=
,OC是半径,利用垂径定理的推论,可知OC⊥AB,在Rt△OAE中,利用三角函数值,可求AE,而AB=2AE,易求AB.
(2)由于AC=BC,那么
 |
| AC |
 |
| BC |
解答:证明:(1)连接OA,(1分)
∵∠B=25°,
∴∠0=2∠B=50°,(2分)
∵∠D=40°,
∴∠D+∠O=90°,(1分)
∴∠OAD=90°,
∴AD是⊙O的切线;(1分)
(2)∵AC=BC,
∴
=
,
∴OC⊥AB,(2分)
∴AE=OAsin50°,(2分)
∴AB=2AE=2×5sin50°≈7.66.(1分)
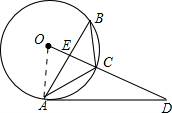
∵∠B=25°,
∴∠0=2∠B=50°,(2分)
∵∠D=40°,
∴∠D+∠O=90°,(1分)
∴∠OAD=90°,
∴AD是⊙O的切线;(1分)
(2)∵AC=BC,
∴
 |
| AC |
 |
| BC |
∴OC⊥AB,(2分)
∴AE=OAsin50°,(2分)
∴AB=2AE=2×5sin50°≈7.66.(1分)

点评:本题利用了圆周角定理、三角形内角和定理、切线的判定、垂径定理的推论、三角函数值.

练习册系列答案
相关题目
 已知:如图,等腰梯形ABCD中,AB∥CD,对角线AC⊥BD于O,BC=13
已知:如图,等腰梯形ABCD中,AB∥CD,对角线AC⊥BD于O,BC=13 8、已知:如图,等腰直角三角形ABC中,∠ACB=90°,直线l经过点C,AD⊥l,BE⊥l,垂足分别为D,E.
8、已知:如图,等腰直角三角形ABC中,∠ACB=90°,直线l经过点C,AD⊥l,BE⊥l,垂足分别为D,E. 24、已知:如图,等腰梯形ABCD中,AD∥BC,BD平分∠ABC.
24、已知:如图,等腰梯形ABCD中,AD∥BC,BD平分∠ABC. 7、已知:如图,等腰△ABC中,AB=AC,AD⊥BC于D,CG∥AB,BG分别交AD、AC于E、F.求证:BE2=EF•EG.
7、已知:如图,等腰△ABC中,AB=AC,AD⊥BC于D,CG∥AB,BG分别交AD、AC于E、F.求证:BE2=EF•EG. 已知:如图,等腰△ABC中,AB=BC,AE⊥BC于E,EF⊥AB于F,cos∠AEF=
已知:如图,等腰△ABC中,AB=BC,AE⊥BC于E,EF⊥AB于F,cos∠AEF=