题目内容
如图所示,在梯形ABCD中,AD∥BC,AB⊥BC,以AB为直径的⊙O与DC相切于E.已 知AB=8,边BC比AD大6.
知AB=8,边BC比AD大6.(1)求边AD、BC的长;
(2)在直径AB上是否存在一动点P,使以A、D、P为顶点的三角形与△BCP相似?若存在,求出AP的长;若不存在,请说明理由.
分析:过D作DF⊥BC于F,设AD=x,则DE=AD=x,EC=BC=x+6,根据勾股定理就得到一个关于x的方程,就可以解得AD的长;△ADP和△BCP相似,有△ADP∽△BCP和△ADP∽△BPC两种情况进行讨论,根据相似三角形的对应边的比相等,就可以求出AP的长.
解答: 解:(1)方法1:过D作DF⊥BC于F,
解:(1)方法1:过D作DF⊥BC于F,
在Rt△DFC中,DF=AB=8,FC=BC-AD=6,
∴DC2=62+82=100,即DC=10.(1分)
设AD=x,则DE=AD=x,EC=BC=x+6,
∴x+(x+6)=10.
∴x=2.
∴AD=2,BC=2+6=8.(4分)
方法2:连OD、OE、OC,
由切线长定理可知∠DOC=90°,AD=DE,CB=CE,
设AD=x,则BC=x+6,
由射影定理可得:OE2=DE•EC.(2分)
即:x(x+6)=16,
解得x1=2,x2=-8,(舍去)
∴AD=2,BC=2+6=8.(4分)
(2)存在符合条件的P点.
设AP=y,则BP=8-y,△ADP与△BCP相似,有两种情况:
①△ADP∽△BCP时,有
=
,即
=
∴y=
;(6分)
②△ADP∽△BPC时,有
=
,即
=
∴y=4.(7分)
故存在符合条件的点P,此时AP=
或4.(8分)
 解:(1)方法1:过D作DF⊥BC于F,
解:(1)方法1:过D作DF⊥BC于F,在Rt△DFC中,DF=AB=8,FC=BC-AD=6,
∴DC2=62+82=100,即DC=10.(1分)
设AD=x,则DE=AD=x,EC=BC=x+6,
∴x+(x+6)=10.
∴x=2.
∴AD=2,BC=2+6=8.(4分)
方法2:连OD、OE、OC,
由切线长定理可知∠DOC=90°,AD=DE,CB=CE,
设AD=x,则BC=x+6,
由射影定理可得:OE2=DE•EC.(2分)
即:x(x+6)=16,
解得x1=2,x2=-8,(舍去)
∴AD=2,BC=2+6=8.(4分)
(2)存在符合条件的P点.
设AP=y,则BP=8-y,△ADP与△BCP相似,有两种情况:
①△ADP∽△BCP时,有
| AD |
| BC |
| AP |
| PB |
| 2 |
| 8 |
| y |
| 8-y |
| 8 |
| 5 |
②△ADP∽△BPC时,有
| AD |
| BP |
| AP |
| BC |
| 2 |
| 8-y |
| y |
| 8 |
故存在符合条件的点P,此时AP=
| 8 |
| 5 |
点评:本题主要考查了相似三角形的判定性质,对应边的比相等的两三角形相似.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
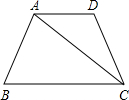 已知如图所示,在梯形ABCD中,AD∥BC,AB=AD=DC=8,∠B=60°,连接AC.
已知如图所示,在梯形ABCD中,AD∥BC,AB=AD=DC=8,∠B=60°,连接AC.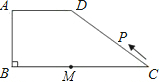 如图所示,在梯形ABCD中,AD∥BC,∠ABC=90°,AD=AB=6,BC=14,点M是线段BC上一定点,且MC=8.动点P从C点出发沿C?D?A?B的路线运动,运动到点B停止.在点P的运动过程中,使△PMC为等腰三角形的点P有
如图所示,在梯形ABCD中,AD∥BC,∠ABC=90°,AD=AB=6,BC=14,点M是线段BC上一定点,且MC=8.动点P从C点出发沿C?D?A?B的路线运动,运动到点B停止.在点P的运动过程中,使△PMC为等腰三角形的点P有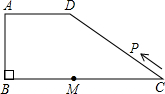 如图所示,在梯形ABCD中,AD∥BC,∠ABC=90°,AD=AB=6,BC=14,点M是线段BC上一定点,且MC=8.动点P从C点出发沿C→D→A→B的路线运动,运动到点B停止.在点P的运动过程中,使△PMC为等腰三角形的点P有几个?并求出相应等腰三角形的腰长.
如图所示,在梯形ABCD中,AD∥BC,∠ABC=90°,AD=AB=6,BC=14,点M是线段BC上一定点,且MC=8.动点P从C点出发沿C→D→A→B的路线运动,运动到点B停止.在点P的运动过程中,使△PMC为等腰三角形的点P有几个?并求出相应等腰三角形的腰长.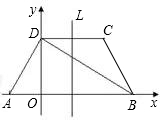 如图所示,在梯形ABCD中,已知AB∥CD,AD⊥DB,AD=DC=CB,AB=4,DO垂直于AB.则腰长是
如图所示,在梯形ABCD中,已知AB∥CD,AD⊥DB,AD=DC=CB,AB=4,DO垂直于AB.则腰长是 如图所示,在梯形ABCD中,AB∥DC,EF是梯形的中位线,AC交EF于G,BD交EF于H,以下说法错误的是( )
如图所示,在梯形ABCD中,AB∥DC,EF是梯形的中位线,AC交EF于G,BD交EF于H,以下说法错误的是( )