题目内容
 如图所示,反比例函数y=
如图所示,反比例函数y=| 6 | x |
分析:反比例函数y=
的图象与正比例函数y=k1x有两个交点,交点的坐标关于原点对称,同理反比例函数y=
的图象与正比例函数y=k2x也有两个交点,交点的坐标也关于原点对称,顺次连接四个点所构成的四边形是对角线互相平分的四边形,故是平行四边形.
| 6 |
| x |
| 6 |
| x |
解答:解:y=
①,y=k1x②,
解由①②组成的方程组,得x=±
,y=±k1
;
即两点的坐标到原点的距离相等,两点又在同一条直线上;
同理y=
③,y=k2x④,
解由③④组成的方程组,同样得到两个点的坐标,两点到原点的距离也相等.
即对角线互相平分的四边形是平行四边形.
| 6 |
| x |
解由①②组成的方程组,得x=±
|
|
即两点的坐标到原点的距离相等,两点又在同一条直线上;
同理y=
| 6 |
| x |
解由③④组成的方程组,同样得到两个点的坐标,两点到原点的距离也相等.
即对角线互相平分的四边形是平行四边形.
点评:本题利用了①反比例函数的图象与正比例函数的图象有交点,则交点关于原点对称;
②对角线互相平分的四边形是平行四边形.
②对角线互相平分的四边形是平行四边形.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
 已知:如图所示,反比例函数y=
已知:如图所示,反比例函数y=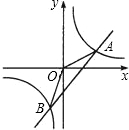 如图所示,反比例函数y=
如图所示,反比例函数y= (2013•石峰区模拟)如图所示,反比例函数
(2013•石峰区模拟)如图所示,反比例函数 二次函数y=ax2+bx+c的图象如图所示,反比例函数y=
二次函数y=ax2+bx+c的图象如图所示,反比例函数y= 如图所示,反比例函数图象上一点A,过A作AB⊥x轴于B,若S△AOB=3,则反比例函数的解析式为
如图所示,反比例函数图象上一点A,过A作AB⊥x轴于B,若S△AOB=3,则反比例函数的解析式为