题目内容
两个完全相同的矩形如图放置，每个矩形的面积为28，图中阴影部分的面积为20，则每个矩形的周长是（ ）| A、18 | B、22 | C、26 | D、32 |
考点：整式的混合运算
专题：
分析：设矩形的长边是a，短边是b，则20=56-
（a+b）a-
ab，求出b，再求出a，即可得出答案．
| 1 |
| 2 |
| 1 |
| 2 |
解答：解：设矩形的长边是a，短边是b，
则20=56-
（a+b）a-
ab，
解得：b=4，
即a=28÷4=7，
所以每个矩形的面积是（4+7）×2=22，
故选B．
则20=56-
| 1 |
| 2 |
| 1 |
| 2 |
解得：b=4，
即a=28÷4=7，
所以每个矩形的面积是（4+7）×2=22，
故选B．
点评：本题考查了矩形性质和三角形的面积的应用，解此题的关键是能把不规则图形的面积转化成规则图形的面积．
练习册系列答案
相关题目
如图，已知⊙P的半径是1，圆心P在抛物线y=x2-2x+1上运动，当⊙P与x轴相切时，圆心P的坐标为一次函数y=kx+b与反比例函数y=
，x与y的对应值如下表：不等式kx+b＜
的解为（ ）
| m |
| x |
| m |
| x |
| x | -3 | -2 | -1 | 1 | 2 | 3 | ||||||
| y=kx+b | 4 | 3 | 2 | 0 | -1 | -2 | ||||||
y=
|
|
1 | 2 | -2 | -1 | -
|
| A、x＜-1或0＜x＜2 |
| B、-1＜x＜0或x＞2 |
| C、x＞-1或x＜2 |
| D、以上答案都不对 |
数据a，4，2，5，3的平均数为b，且a和b是方程x2-4x+3=0的两个根，则b是（ ）
| A、1 | B、3 | C、2 | D、2.5 |
式子
在实数范围内有意义，则x的取值范围是（ ）
| -3+x |
| A、x≥3 | B、x≤3 |
| C、x≠3 | D、x≤-3 |
从五个点（-2，4）、（4，2）、（2，3）、（2，-4）、（1，-8）中任取一点，在直线y=-
上的概率是（ ）
| 8 |
| x |
A、
| ||
B、
| ||
C、
| ||
D、
|
在“体育中考”的某次模拟测试中，某校某班10名学生测试成绩统计如图．对于这10名学生的参赛成绩，下列说法中错误的是（ ）| A、众数是28 |
| B、中位数是28 |
| C、平均数是27.5 |
| D、极差是8 |
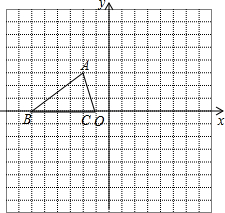如图，已知△ABC的三个顶点的坐标分别为A（-2，3）、B（-6，0）、C（-1，0）．