题目内容
【题目】过反比例函数![]() (
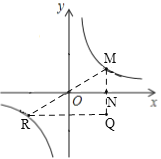
(![]() )图像上一动点M作MN⊥x轴交x轴于点N,Q是直线MN上一点,且MQ=2MN,过点Q作QR∥
)图像上一动点M作MN⊥x轴交x轴于点N,Q是直线MN上一点,且MQ=2MN,过点Q作QR∥![]() 轴交该反比例函数图像于点R,已知S△QRM=8,那么k的值为_____.
轴交该反比例函数图像于点R,已知S△QRM=8,那么k的值为_____.
【答案】12或4
【解析】
由k>0,可知点M在第一象限或第三象限,设点M的坐标为(m,![]() ),分别讨论点Q所在象限,根据MQ=2MN,用m、k表示出点Q和点R的坐标,利用S△QRM=8,即可得出k的值.
),分别讨论点Q所在象限,根据MQ=2MN,用m、k表示出点Q和点R的坐标,利用S△QRM=8,即可得出k的值.
∵k>0,
∴点M在第一象限或第三象限,
点M在第一象限时,设点M的坐标为(m,![]() ),
),
①如图,当点Q在第一象限时,
∵MQ=2MN,
∴QN=3MN,
∴点Q坐标为(m,![]() ),
),
∵QR//x轴,点R在反比例函数上,
∴点R坐标为(![]() ,
,![]() ),
),
∴QR=m-![]() =
=![]() ,QM=
,QM=![]() -
-![]() =
=![]() ,
,
∵S△QRM=8,
∴![]()
![]()
![]()
![]()
![]() =8,
=8,
解得:k=12.
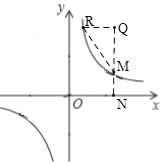
②如图,当点Q在第四象限时,
∵MQ=2MN,
∴MN=NQ,
∴点Q坐标为(m,-![]() ),
),
∵QR//x轴,点R在反比例函数上,
∴点R坐标为(-m,-![]() ),
),
∴QR=m-(-m)=2m,QM=![]() -(-
-(-![]() )=
)=![]() ,
,
∵∵S△QRM=8,
∴![]()
![]() 2m
2m![]()
![]() =8,
=8,
解得:k=4,
同理可得:点M在第三象限时k=4或k=12,
综上所述:k的值为12或4.
故答案为:12或4.

练习册系列答案
相关题目