题目内容
阅读材料:如图1,在△AOB中,∠O=90°,OA=OB,点P在AB边上,PE⊥OA于点E,PF⊥OB于点F,则PE+PF=OA.(此结论不必证明,可直接应用)

(1)【理解与应用】
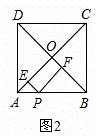
如图2,正方形ABCD的边长为2,对角线AC,BD相交于点O,点P在AB边上,PE⊥OA于点E,PF⊥OB于点F,则PE+PF的值为  .
.
(2)【类比与推理】
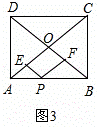
如图3,矩形ABCD的对角线AC, BD相交于点O,AB=4,AD=3,点P在AB边上,PE∥OB交AC于点E,PF∥OA交BD于点F,求PE+PF的值;
BD相交于点O,AB=4,AD=3,点P在AB边上,PE∥OB交AC于点E,PF∥OA交BD于点F,求PE+PF的值;
(3)【拓展与延伸】
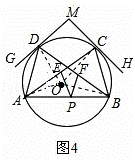
如图4,⊙O的半径为4,A,B,C, D是⊙O上的四点,过点C,D的切线CH,DG相交于点M,点P在弦AB上,PE∥BC交AC于点E,PF∥AD于点F,当∠ADG=∠BCH=30°时,PE+PF是否为定值?若是,请求出这个定值;若不是,请说明理由.
D是⊙O上的四点,过点C,D的切线CH,DG相交于点M,点P在弦AB上,PE∥BC交AC于点E,PF∥AD于点F,当∠ADG=∠BCH=30°时,PE+PF是否为定值?若是,请求出这个定值;若不是,请说明理由.
解:(1)如图2,
∵四边形ABCD是正方形,
∴OA=OB=OC=OD,∠ABC=∠AOB=90°.
∵AB=BC=2,
∴AC=2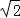 .
.
∴OA=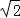 .
.
∵OA=OB,∠AOB=90°,PE⊥OA,PF⊥OB,
∴PE+PF=OA=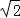 .
.
(2)如图3,
∵四边形ABCD是矩形,
∴OA=OB=OC=OD,∠DAB=90°.
∵AB=4,AD=3,
∴BD=5.
∴OA=OB=OC=OD=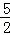 .
.
∵PE∥OB,P F∥AO,
F∥AO,
∴△AEP∽△AOB,△BFP∽△BOA.
∴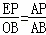 ,
,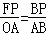 .
.
∴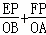 =
=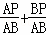 =1.
=1.
∴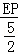 +
+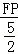 =1.
=1.
∴EP+FP=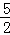 .
.
∴PE+PF的值为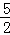 .
.
(3)当∠ADG=∠BCH=30°时,PE+PF是定值.
理由:连接OA、OB、OC、OD,如图4.
∵DG与⊙O相切,
∴∠GDA=∠ABD.
∵∠ADG=3 0°,
0°,
∴∠ABD=30°.
∴∠AOD=2∠ABD=60°.
∵OA=OD,
∴△AOD是等边三角形.
∴AD=OA=4.
同理可得:BC=4.
∵PE∥BC,PF∥AD,
∴△AEP∽△ACB,△BFP∽△BDA.
∴ ,
,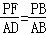 .
.
∴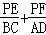 =
=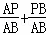 =1.
=1.
∴ =1.
=1.
∴PE+PF=4.
∴当∠ADG=∠BCH=30°时,PE+PF=4.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案如表是10支不同型号签字笔的相关信息,则这10支签字笔的平均价格是( )
| 型号 | A | B | C |
| 价格(元/支) | 1 | 1.5 | 2 |
| 数量(支) | 3 | 2 | 5 |
|
| A. | 1.4元 | B. | 1.5元 | C. | 1.6元 | D. | 1.7元 |
 BC,求证:四边形OCFE是平行四边形.
BC,求证:四边形OCFE是平行四边形.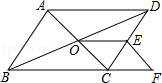
 所在象限内,y的值随x值的增大而减小,则满足条件的一个数值k为
所在象限内,y的值随x值的增大而减小,则满足条件的一个数值k为 
 ,则
,则 的度数是
的度数是 B.
B. C.
C. D.
D.

 (x﹣6)2+4,则选取点B为坐标原点时的抛物线解析式是 .
(x﹣6)2+4,则选取点B为坐标原点时的抛物线解析式是 .