题目内容
如图,AB是⊙O的直径,AE是弦,C是劣弧AE的中点,过C作CD⊥AB于点D,CD交AE于点F,过C作CG∥AE交BA的延长线于点G
(1) 求证:CG是⊙O的切线
(2) 求证:AF=CF
(3) 若∠EAB=30°,CF=2 求AG的长

解:(1)连接CO
∵  =
=
∴OC⊥AE
∵AE//CG
∴OC⊥CG ∵OC为半径
∴CG是圆O的切线 ------------------------3分
(2)连接AC·BC
∵AB是直径
∴∠ACB=90°
∴∠ACD+∠DCB=90°
∵CD⊥AB
∴∠CDB=90°
∴∠DCB+∠CBD=90°
∴∠ACD=∠CBD
∵  =
=
∴∠CAE=∠CBD
∴∠ACD=∠CAE
∴AF=CF ------------------------------------7分
(3)∵AF=CF CF=2
∴AF=2
∵∠EAB=30°
∴在RT△AFD中FD=AF·sin30°=2×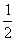 =1
=1
AD=AF×co s30°=2×
s30°=2× =
=
∵CG//AE
∴ =
=
∴ =
=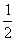 ∴AG=2
∴AG=2 -------------------------------------------------10分
-------------------------------------------------10分

巴中市对初三年级学生的体育、物理实验操作、化学实验操作成绩进行抽样调查,成绩评定为A、B、C、D四个等级,现抽取这 三种成绩共1 000份进行统计分析,其中A、B、C、D分别表示优秀、良好、合格、不合格四个等级,相关数据统计如表、图所示.
三种成绩共1 000份进行统计分析,其中A、B、C、D分别表示优秀、良好、合格、不合格四个等级,相关数据统计如表、图所示.
| A | B | C | D | |
| 物理实验操作 | 120 |
| 90 | 20 |
| 化学实验操作 | 90 | 110 | 30 |
|
| 体育 |
| 140 | 160 | 27 |

(1)请将表补充完整(直接填数据,不写解答过程);
(2)巴中市共有40 000名学生参加测试,试估计该市初三年级学生化学实验操作合格及合格以上大约有多少人?
(3)在这40 000名学生中,体育成绩不合格的大约有多少人?
中心对称与中心对称图形
| 中心对称 | 中心对称图形 | |
| 定义 | 把一个图形绕着一点旋转 | 把一个图形绕着某点旋转 |
| 区别 | 中心对称是指两个全等图形之间的相互位置关系. | 中心对称图形是指具有特殊形状的一个图形. |
| 中心对称的性质 | 1.中心对称的两个图形,对称点所连线段都经过 2.成中心对称的两个图形 |

 —4xy=
—4xy= 

 后,如果与另一个图形重合,那么这两个图形成中心对称,这个点叫做其对称中心,旋转前后重合的点叫做对称点.
后,如果与另一个图形重合,那么这两个图形成中心对称,这个点叫做其对称中心,旋转前后重合的点叫做对称点. 后,能与其自身重合,那么这个图形叫做中心对称图形,这个点叫做
后,能与其自身重合,那么这个图形叫做中心对称图形,这个点叫做 .
.
 ,而且被对称中心
,而且被对称中心 ;
; .
.

 =
= ,△ADE的面积是8,则△ABC的面积为 .
,△ADE的面积是8,则△ABC的面积为 .