题目内容
如图,A、B是反比例函数y= 上两点,AC⊥y轴于C,BD⊥x轴于D,AC=BD=
上两点,AC⊥y轴于C,BD⊥x轴于D,AC=BD= OC,S四边形ABDC=9,则k= .
OC,S四边形ABDC=9,则k= .
【答案】分析:如图,分别延长CA、DB交于点E,由于AC⊥y轴于C,BD⊥x轴于D,AC=BD= OC,设AC=t,则BD=t,OC=5t,即点A的坐标为(t,5t),而A、B是反比例函数y=
OC,设AC=t,则BD=t,OC=5t,即点A的坐标为(t,5t),而A、B是反比例函数y= 上两点,
上两点,
则OD•t=t•5t,所以点B的坐标为(5t,t),S根据四边形ABDC=S△ECD-S△EAB,即 5t•5t-
5t•5t- 4t•4t=9,解得t2=2,所以k=t•5t=10.
4t•4t=9,解得t2=2,所以k=t•5t=10.
解答:解:如图,分别延长CA、DB交于点E,
∵AC⊥y轴于C,BD⊥x轴于D,AC=BD= OC,
OC,
∴点A的横坐标与点B的纵坐标相等,
设AC=t,则BD=t,OC=5t,即点A的坐标为(t,5t),
∴A、B是反比例函数y= 上两点,
上两点,
∴OD•t=t•5t,
∴点B的坐标为(5t,t),
∴AE=5t-t=4t,BE=5t-t=4t,
∴S四边形ABDC=S△ECD-S△EAB,
∴ 5t•5t-
5t•5t- 4t•4t=9,
4t•4t=9,
∴t2=2,
∴k=t•5t=10.
故答案为10.
点评:本题考查了反比例函数y= (k≠0)系数k的几何意义:从反比例函数y=
(k≠0)系数k的几何意义:从反比例函数y= (k≠0)图象上任意一点向x轴和y轴作垂线,垂线与坐标轴所围成的矩形面积为|k|.
(k≠0)图象上任意一点向x轴和y轴作垂线,垂线与坐标轴所围成的矩形面积为|k|.
 OC,设AC=t,则BD=t,OC=5t,即点A的坐标为(t,5t),而A、B是反比例函数y=
OC,设AC=t,则BD=t,OC=5t,即点A的坐标为(t,5t),而A、B是反比例函数y= 上两点,
上两点,则OD•t=t•5t,所以点B的坐标为(5t,t),S根据四边形ABDC=S△ECD-S△EAB,即
 5t•5t-
5t•5t- 4t•4t=9,解得t2=2,所以k=t•5t=10.
4t•4t=9,解得t2=2,所以k=t•5t=10.解答:解:如图,分别延长CA、DB交于点E,

∵AC⊥y轴于C,BD⊥x轴于D,AC=BD=
 OC,
OC,∴点A的横坐标与点B的纵坐标相等,
设AC=t,则BD=t,OC=5t,即点A的坐标为(t,5t),
∴A、B是反比例函数y=
 上两点,
上两点,∴OD•t=t•5t,
∴点B的坐标为(5t,t),
∴AE=5t-t=4t,BE=5t-t=4t,
∴S四边形ABDC=S△ECD-S△EAB,
∴
 5t•5t-
5t•5t- 4t•4t=9,
4t•4t=9,∴t2=2,
∴k=t•5t=10.
故答案为10.
点评:本题考查了反比例函数y=
 (k≠0)系数k的几何意义:从反比例函数y=
(k≠0)系数k的几何意义:从反比例函数y= (k≠0)图象上任意一点向x轴和y轴作垂线,垂线与坐标轴所围成的矩形面积为|k|.
(k≠0)图象上任意一点向x轴和y轴作垂线,垂线与坐标轴所围成的矩形面积为|k|. 
练习册系列答案
相关题目
 如图所示,P是反比例函数图象在第二象限上的一点,且矩形PEOF的面积为3,则反比例函数的表达式是( )
如图所示,P是反比例函数图象在第二象限上的一点,且矩形PEOF的面积为3,则反比例函数的表达式是( )A、y=
| ||
B、y=
| ||
C、y=-
| ||
D、y=-
|
 如图,A、B是反比例函数y=
如图,A、B是反比例函数y=| k |
| x |
| A、S△ADB>S△ACB |
| B、S△ADB<S△ACB |
| C、S△ADB=S△ACB |
| D、不确定 |
 如图所示,P是反比例函数
如图所示,P是反比例函数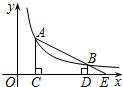 如图,A,B是反比例函数y=
如图,A,B是反比例函数y= 如图,若点P是反比例函数y=
如图,若点P是反比例函数y=