题目内容
如图,直线y=-| 3 |
| 4 |
| 5 |
| 4 |
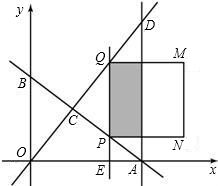 .
.(1)求点C的坐标.
(2)当0<t<5时,求S与t之间的函数关系式.
(3)求(2)中S的最大值.
(4)当t>0时,直接写出点(4,
| 9 |
| 2 |
参考公式:二次函数y=ax2+bx+c图象的顶点坐标为(-
| b |
| 2a |
| 4ac-b2 |
| 4a |
分析:(1)简单求两直线的交点,得点C的坐标;
(2)根据几何关系把s用t表示,注意当MN在AD上时,这一特殊情况.
(3)转化为求函数最值问题;
(4)求定点在正方形PQMN内部时,t的范围,点E在x轴上运动,要用到分类讨论.
(2)根据几何关系把s用t表示,注意当MN在AD上时,这一特殊情况.
(3)转化为求函数最值问题;
(4)求定点在正方形PQMN内部时,t的范围,点E在x轴上运动,要用到分类讨论.
解答:解:(1)由题意,得
,
解得
,
∴C(3,
).
(2)根据题意,得AE=t,OE=8-t.
∴点Q的纵坐标为
(8-t),点P的纵坐标为-
(8-t)+6=
t,
∴PQ=
(8-t)-
t=10-2t.
当MN在AD上时,10-2t=t,
∴t=
.
当0<t≤
时,S=t(10-2t),即S=-2t2+10t.
当
<t<5时,S=(10-2t)2,即S=4t2-40t+100.
(3)当0<t≤
时,S=-2(t-
)2+
,
∴t=
时,S最大值=
.
当
≤t<5时,S=4(t-5)2,
∵t<5时,S随t的增大而减小,
∴t=
时,S最大值=
.
∵
>
,
∴S的最大值为
.
(4)当t=5时,PQ=0,P,Q,C三点重合;
当t<5时,知OE=4时是临界条件,即8-t=4
即t=4
∴点Q的纵坐标为5>
,
点(4,
)在正方形边界PQ上,E继续往左移动,则点(4,
)进入正方形内部,但点Q的纵坐标再减少,当Q点的纵坐标为
时,OE=
∴8-t=
即t=
,
此时OE+PN=
+PQ=
+(10-2t)=
>4满足条件,
∴4<t<
,
当t>5时,由图和条件知,则有E(t-8,0),PQ=2t-10要满足点(4,
)在正方形的内部,
则临界条件N点横坐标为4?4=PQ+OE=|2t-10|+|t-8|=3t-18
即t=6,此时Q点的纵坐标为:-
×2+6=
.满足条件,
∴t>6.
综上所述:4<t<
或t>6.
|
解得
|
∴C(3,
| 15 |
| 4 |
(2)根据题意,得AE=t,OE=8-t.
∴点Q的纵坐标为
| 5 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |

∴PQ=
| 5 |
| 4 |
| 3 |
| 4 |
当MN在AD上时,10-2t=t,
∴t=
| 10 |
| 3 |
当0<t≤
| 10 |
| 3 |
当
| 10 |
| 3 |
(3)当0<t≤
| 10 |
| 3 |
| 5 |
| 2 |
| 25 |
| 2 |
∴t=
| 5 |
| 2 |
| 25 |
| 2 |
当
| 10 |
| 3 |
∵t<5时,S随t的增大而减小,
∴t=
| 10 |
| 3 |
| 100 |
| 9 |
∵
| 25 |
| 2 |
| 100 |
| 9 |
∴S的最大值为
| 25 |
| 2 |
(4)当t=5时,PQ=0,P,Q,C三点重合;

当t<5时,知OE=4时是临界条件,即8-t=4
即t=4
∴点Q的纵坐标为5>
| 9 |
| 2 |
点(4,
| 9 |
| 2 |
| 9 |
| 2 |
| 9 |
| 2 |
| 18 |
| 5 |
∴8-t=
| 18 |
| 5 |
| 22 |
| 5 |
此时OE+PN=
| 18 |
| 5 |
| 18 |
| 5 |
| 24 |
| 5 |
∴4<t<
| 22 |
| 5 |
当t>5时,由图和条件知,则有E(t-8,0),PQ=2t-10要满足点(4,
| 9 |
| 2 |
则临界条件N点横坐标为4?4=PQ+OE=|2t-10|+|t-8|=3t-18
即t=6,此时Q点的纵坐标为:-
| 3 |
| 4 |
| 9 |
| 2 |
∴t>6.
综上所述:4<t<
| 22 |
| 5 |
点评:此题前三问简单,考查函数基本性质,求函数最值问题,第四问考查动点问题,求t的范围,观察图形,搞清几何坐标,理清思路,又运用分类讨论思想.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
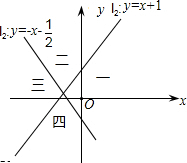 如图,直线l1:y=x+1与直线l2:y=-x-
如图,直线l1:y=x+1与直线l2:y=-x-| 1 |
| 2 |
| 3 |
| 4 |
| 1 |
| 2 |
| A、第一部分 | B、第二部分 |
| C、第三部分 | D、第四部分 |
 14、如图,直线AB、CD交于O点,OE为∠AOC的平分线,∠1=17°,则∠2=
14、如图,直线AB、CD交于O点,OE为∠AOC的平分线,∠1=17°,则∠2=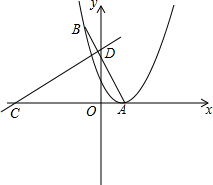 (2012•江汉区模拟)已知:抛物线
(2012•江汉区模拟)已知:抛物线 (2009•无锡二模)如图,直线L1∥L2,AB⊥CD,∠1=34°,那么∠2的度数是
(2009•无锡二模)如图,直线L1∥L2,AB⊥CD,∠1=34°,那么∠2的度数是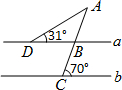 (2012•广州模拟)如图,直线a∥b,则∠A的度数是( )
(2012•广州模拟)如图,直线a∥b,则∠A的度数是( )