Question

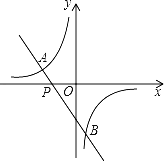
【题目】如图，已知点A，B，C，D均在⊙O上，CD为∠ACE的角平分线．

（1）求证：△ABD为等腰三角形；

（2）若∠DCE=45°，BD=6，求⊙O的半径．

Answer 1

【答案】（1）证明见解析（2）3

【解析】试题分析：（1）欲证明△ABD为等腰三角形，只要证明∠DBA=∠DAB即可．

（2）如图2中，只要证明AB是直径即可解决问题．

试题解析：（1）如图1中，

∵CD平分∠EAC，

∴∠ECD=∠DCA，

∵∠ECD=∠DAB，∠DCA=∠DBA，

∴∠DBA=∠DAB，

∴DB=DA．

∵△DBA是等腰三角形．

（2）如图2中，

∵∠DCE=∠DCA=45°，

∴∠ECA=∠ACB=90°，

∴AB是直径，

∴∠BDA=90°，

∵BD=AD=6，

∴AB=．

∴⊙O的半径为3.