题目内容
(2012•黄冈模拟)如图,在Rt△AOB中,∠AOB=90°,OA=3cm,OB=4cm,以点O为坐标原点建立坐标系,设P,Q分别为AB,OB边上的动点,它们同时分别从点A,O向B点匀速运动, 速度均为1厘米/秒,设移动的时间为t(0≤t≤4)秒.
速度均为1厘米/秒,设移动的时间为t(0≤t≤4)秒.
(1)求运动t秒时,P,Q两点的坐标.(用含t的式子表示).
(2)若△OPQ的面积为Scm2,运动的时间为t秒,求S与t之间的函数关系式.当t为何值时,S有最大值?最大面积是多少?
(3)当t为何值时,直线PQ将△AOB的面积分成1:3两部分?
(4)按此速度运动下去,△OPQ能否成为正三角形?若能,求出时间t;若不能,请说明理由.能否通过改变Q点的速度,使△OPQ成为正三角形?若能,请求出改变后Q的速度和此时t的值.
 速度均为1厘米/秒,设移动的时间为t(0≤t≤4)秒.
速度均为1厘米/秒,设移动的时间为t(0≤t≤4)秒.(1)求运动t秒时,P,Q两点的坐标.(用含t的式子表示).
(2)若△OPQ的面积为Scm2,运动的时间为t秒,求S与t之间的函数关系式.当t为何值时,S有最大值?最大面积是多少?
(3)当t为何值时,直线PQ将△AOB的面积分成1:3两部分?
(4)按此速度运动下去,△OPQ能否成为正三角形?若能,求出时间t;若不能,请说明理由.能否通过改变Q点的速度,使△OPQ成为正三角形?若能,请求出改变后Q的速度和此时t的值.
分析:(1)作PM⊥OA于M,则PM∥OB,再根据平行线分线段成比例定理列出比例式;由勾股定理求出AB=5,而AP=t,根据比例式求出AM、PM的值,P点坐标即可得到,由
(2)根据三角形的面积公式,P点纵坐标与OQ的长度的积的一半就是△OPQ面积,整理后根据二次函数的最值问题求解即可;
(3)因为S△ABO=
OA×OB=
×3×4=6,又S△PQB=
BQ×Py=
×(4-t)(3-
t),若直线PQ将△AOB的面积分成1:3两部分
则当
×(4-t)(3-
t)=
×6或
×(4-t)(3-
t)=
×6,分别求出符合题意的t值即可;
(4)按此速度运动下去,△OPQ不能成为正三角形根据正三角形的性质PN垂直平分边OQ,所以无论t为何值时,△OPQ都不可能为正三角形;改变Q点速度根据正三角形的性质,0Q=2ON,PN=
OQ,分别列式求解即可得到Q点运动速度和时间t.
(2)根据三角形的面积公式,P点纵坐标与OQ的长度的积的一半就是△OPQ面积,整理后根据二次函数的最值问题求解即可;
(3)因为S△ABO=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 5 |
则当
| 1 |
| 2 |
| 3 |
| 5 |
| 1 |
| 4 |
| 1 |
| 2 |
| 3 |
| 5 |
| 3 |
| 4 |
(4)按此速度运动下去,△OPQ不能成为正三角形根据正三角形的性质PN垂直平分边OQ,所以无论t为何值时,△OPQ都不可能为正三角形;改变Q点速度根据正三角形的性质,0Q=2ON,PN=
| ||
| 2 |
解答:解:(1)作PM⊥OA于M,则PM∥OB,
∴AM:AO=PM:BO=AP:AB,
∵OA=3cm,OB=4cm,
∴在Rt△OAB中,AB=
=5=5cm,
∵AP=1•t=t,
∴
=
=
,
∴PM=
t,AM=
t,
∴OM=OA-AM=3-
t,
∴点P的坐标为(
t,3-
t),
∵Q点的运动速度是速度为1厘米/秒,
∴OQ=1×t,
∴Q的坐标是(t,0);
(2)OQ=1•t=tcm,
∴S△OPQ=
×t×(3-
t)=-
(t-
)2+
,
∵a=-
<0,
∴当t=
时,S最大=
;
(3)∵S△ABO=
OA×OB=
×3×4=6,
又S△PQB=
BQ×Py=
×(4-t)(3-
t),
当
×(4-t)(3-
t)=
×6时,则t=
(舍去)或
;
当
×(4-t)(3-
t)=
×6时,则t=
(舍去)或
,
∴当t=
或
时,直线PQ将△AOB的面积分成1:3两部分;
(4)按此速度运动下去,△OPQ不能成为正三角形,理由如下:过点P作PN⊥OQ,
∵OP2=PN2+ON2=PN2+(
t)2,QP2=PN2+QN2=PN2+(
t)2,
要使△OPQ成为等边三角形,则PN2+(
t)2=PN2+(
t)2,
∴t=0,但此时不存在三角形,
∴按此速度运动下去,△OPQ不能成为正三角形,
设Q点运动的速度为k,若△OPQ为正三角形,则OP=PQ=OQ,OQ=2ON,
∴kt=2×
t,k=
,
此时PN=OP•sin60°=
OP=
OQ,
即:3-
t=
×
t,
解得:t=
,
∴当Q的运动速度为
cm/s是,△△OPQ成为正三角形,此时t=
.
∴AM:AO=PM:BO=AP:AB,
∵OA=3cm,OB=4cm,
∴在Rt△OAB中,AB=
| OA2+OB2 |
∵AP=1•t=t,
∴
| AM |
| 3 |
| PM |
| 4 |
| t |
| 5 |
∴PM=
| 4 |
| 5 |
| 3 |
| 5 |
∴OM=OA-AM=3-
| 3 |
| 5 |
∴点P的坐标为(
| 4 |
| 5 |
| 3 |
| 5 |
∵Q点的运动速度是速度为1厘米/秒,

∴OQ=1×t,
∴Q的坐标是(t,0);
(2)OQ=1•t=tcm,
∴S△OPQ=
| 1 |
| 2 |
| 3 |
| 5 |
| 3 |
| 10 |
| 5 |
| 2 |
| 15 |
| 8 |
∵a=-
| 3 |
| 10 |
∴当t=
| 5 |
| 2 |
| 15 |
| 8 |
(3)∵S△ABO=
| 1 |
| 2 |
| 1 |
| 2 |
又S△PQB=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 5 |
当
| 1 |
| 2 |
| 3 |
| 5 |
| 1 |
| 4 |
9+
| ||
| 2 |
9-
| ||
| 2 |
当
| 1 |
| 2 |
| 3 |
| 5 |
| 3 |
| 4 |
9+
| ||
| 2 |
9-
| ||
| 2 |
∴当t=
9-
| ||
| 2 |
9-
| ||
| 2 |
(4)按此速度运动下去,△OPQ不能成为正三角形,理由如下:过点P作PN⊥OQ,
∵OP2=PN2+ON2=PN2+(
| 4 |
| 5 |
| 1 |
| 5 |
要使△OPQ成为等边三角形,则PN2+(
| 4 |
| 5 |
| 1 |
| 5 |
∴t=0,但此时不存在三角形,
∴按此速度运动下去,△OPQ不能成为正三角形,
设Q点运动的速度为k,若△OPQ为正三角形,则OP=PQ=OQ,OQ=2ON,
∴kt=2×
| 4 |
| 5 |
| 8 |
| 5 |
此时PN=OP•sin60°=
| ||
| 2 |
| ||
| 2 |
即:3-
| 3 |
| 5 |
| ||
| 2 |
| 8 |
| 5 |
解得:t=
20
| ||
| 13 |
∴当Q的运动速度为
| 8 |
| 5 |
20
| ||
| 13 |
点评:此题考查了勾股定理、相似三角形对应边成比例的性质、等边三角形的高与底边的性质,二次函数最值问题以及相似三角形的判定与性质等知识.此题综合性很强,难度较大,解题的关键是数形结合思想与函数思想的应用,注意辅助线的作法,只要肯于动脑也不难解决.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2012•黄冈模拟)如图所示,一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.下列说法中错误的是( )
(2012•黄冈模拟)如图所示,一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.下列说法中错误的是( )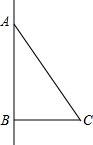 (2012•黄冈模拟)如图,Rt△ABC的两直角边AB=4cm,BC=3cm.以AB所在直线为轴,将△ABC旋转一周后所得几何体的侧面展开图的面积是
(2012•黄冈模拟)如图,Rt△ABC的两直角边AB=4cm,BC=3cm.以AB所在直线为轴,将△ABC旋转一周后所得几何体的侧面展开图的面积是